如图,数轴上有 、 、 三点, 为原点, 、 分别表示仙女座星系、 黑洞与地球的距离(单位:光年).下列选项中,与点 表示的数最为接近的是

A. B. C. D.
数轴上点 , , 表示的数分别是 , ,9,点 为线段 的中点,则 的值是
A.3B.4.5C.6D.18
数轴上点 表示的数是 ,将点 在数轴上平移7个单位长度得到点 .则点 表示的数是
A.4B. 或10C. D.4或
如图,在数轴上,点 、 分别表示数1、 .
(1)求 的取值范围;
(2)数轴上表示数 的点应落在 .
.点 的左边 .线段 上 .点 的右边

如图,将数轴上 与6两点间的线段六等分,这五个等分点所对应数依次为 , , , , ,则下列正确的是

| A. |
|
B. |
|
| C. |
|
D. |
|
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .
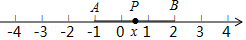
的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;
③当 为何值时,代数式 的最小值是2.
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式 的解集
(1)探究 的几何意义
如图①,在以 为原点的数轴上,设点 对应的数是 ,由绝对值的定义可知,点 与点 的距离为 ,可记为 .将线段 向右平移1个单位得到线段 ,此时点 对应的数是 ,点 对应的数是1.因为 ,所以 .因此, 的几何意义可以理解为数轴上 所对应的点 与1所对应的点 之间的距离 .
(2)求方程 的解
因为数轴上3和 所对应的点与1所对应的点之间的距离都为2,所以方程的解为3, .
(3)求不等式 的解集
因为 表示数轴上 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数 的范围.
请在图②的数轴上表示 的解集,并写出这个解集.
探究二:探究 的几何意义
(1)探究 的几何意义
如图③,在直角坐标系中,设点 的坐标为 ,过 作 轴于 ,作 轴于 ,则 点坐标为 , 点坐标为 , , ,在 中, ,则 ,因此, 的几何意义可以理解为点 与点 之间的距离 .
(2)探究 的几何意义
如图④,在直角坐标系中,设点 的坐标为 ,由探究二(1)可知, ,将线段 先向右平移1个单位,再向上平移5个单位,得到线段 ,此时点 的坐标为 ,点 的坐标为 ,因为 ,所以 ,因此 的几何意义可以理解为点 与点 之间的距离 .
(3)探究 的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为: .
拓展应用:
(1) 的几何意义可以理解为:点 与点 的距离和点 与点 (填写坐标)的距离之和.
(2) 的最小值为 (直接写出结果)

如图,数轴上点 对应的数是 ,将点 沿数轴向左移动2个单位至点 ,则点 对应的数是
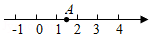
A. B. C. D.
试题篮
()