如图,一个点从数轴上的原点开始,先向左移动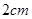 到达
到达 点,再向左移动
点,再向左移动 到达
到达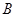 点,然后向右移动
点,然后向右移动 到达
到达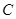 点.
点.
(1)用1个单位长度表示 ,请你在数轴上表示出
,请你在数轴上表示出 、
、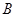 、
、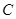 三点的位置;
三点的位置;
(2)把点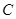 到点
到点 的距离记为
的距离记为 ,则
,则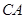 =
= 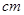 .
.
(3)阅读理解:观察式子: 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
问题解决
若点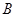 以每秒
以每秒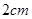 的速度向左移动,同时
的速度向左移动,同时 、
、 点分别以每秒
点分别以每秒 、
、 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为 秒,试探索:
秒,试探索: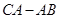 的值是否会随着
的值是否会随着 的变化而改变?请说明理由.
的变化而改变?请说明理由.
如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图1-8并思考,完成下列各题:
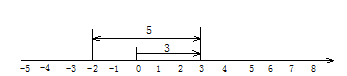
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_______,A,B两点间的距离是________;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是_______,A,B两点间的距离为________;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_________,A,B两点间的距离是________.
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么,请你猜想终点B表示什么数?A,B两点间的距离为多少?
如图,甲、乙两人(看成点)分别在数轴和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率;
(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对次,且他最终停留的位置对应的数为
,试用含
的代数式表示
,并求该位置距离原点
最近时
的值;
(3)从如图的位置开始,若进行了次移动游戏后,甲与乙的位置相距2个单位,直接写出
的值.

如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.

(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则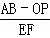 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).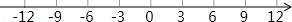
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式 的几何意义是数轴上 所对应的点与2所对应的点之间的距离:因为 ,所以 的几何意义就是数轴上 所对应的点与 所对应的点之间的距离.
(1)发现问题:代数式 的最小值是多少?
(2)探究问题:如图,点 、 、 分别表示数 、2、 , .
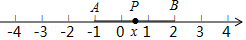
的几何意义是线段 与 的长度之和,
当点 在线段 上时, ,当点 在点 的左侧或点 的右侧时, .
的最小值是3.
(3)解决问题:
① 的最小值是 ;
②利用上述思想方法解不等式: ;
③当 为何值时,代数式 的最小值是2.
如图,已知数轴上有A、B两点(点A在点B的左侧),且两点距离为6个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)图中如果点A、B表示的数是互为相反数,那么点A表示的数是 ;
(2)当t=2秒时,点A与点P之间的距离是 个长度单位;
(3)当点A为原点时,点P表示的数是 ;(用含t的代数式表示)
(4)当t= 秒时,点P到点A的距离是点P到点B的距离的2倍.
在一条不完整的数轴上从左到右有点,
,
,其中
,
,如图所示,设点
,
,
所对应数的和是
.
(1)若以为原点,写出点
,
所对应的数,并计算
的值;若以
为原点,
又是多少?
(2)若原点在图中数轴上点
的右边,且
,求
.

如图,在数轴上,点 、 分别表示数1、 .
(1)求 的取值范围;
(2)数轴上表示数 的点应落在 .
.点 的左边 .线段 上 .点 的右边

元旦放假时,小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了6千米到超市买东西,然后又向东走了1.5千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式 的解集
(1)探究 的几何意义
如图①,在以 为原点的数轴上,设点 对应的数是 ,由绝对值的定义可知,点 与点 的距离为 ,可记为 .将线段 向右平移1个单位得到线段 ,此时点 对应的数是 ,点 对应的数是1.因为 ,所以 .因此, 的几何意义可以理解为数轴上 所对应的点 与1所对应的点 之间的距离 .
(2)求方程 的解
因为数轴上3和 所对应的点与1所对应的点之间的距离都为2,所以方程的解为3, .
(3)求不等式 的解集
因为 表示数轴上 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数 的范围.
请在图②的数轴上表示 的解集,并写出这个解集.
探究二:探究 的几何意义
(1)探究 的几何意义
如图③,在直角坐标系中,设点 的坐标为 ,过 作 轴于 ,作 轴于 ,则 点坐标为 , 点坐标为 , , ,在 中, ,则 ,因此, 的几何意义可以理解为点 与点 之间的距离 .
(2)探究 的几何意义
如图④,在直角坐标系中,设点 的坐标为 ,由探究二(1)可知, ,将线段 先向右平移1个单位,再向上平移5个单位,得到线段 ,此时点 的坐标为 ,点 的坐标为 ,因为 ,所以 ,因此 的几何意义可以理解为点 与点 之间的距离 .
(3)探究 的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为: .
拓展应用:
(1) 的几何意义可以理解为:点 与点 的距离和点 与点 (填写坐标)的距离之和.
(2) 的最小值为 (直接写出结果)

已知数轴上有A、B、C三点,分别代表﹣24,﹣10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
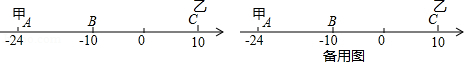
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(1)若 ,求点C到原点的距离;
,求点C到原点的距离;
(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问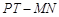 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
试题篮
()