.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm
求y与x之间的关系式.
求当边长增加多少时,面积增加8 cm
随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱.如果按照方案一配货,请你计算出经销商能盈利多少元?
请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
若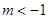 ,则下列函数:①
,则下列函数:①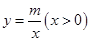 ,②
,②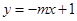 ,③
,③ ,
,
④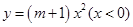 中,
中,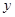 随
随 的增大而增大的函数有( ▲ )
的增大而增大的函数有( ▲ )
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
如图所示的程序是函数型的数值转换程序,其中-2≤x≤2,若输入的x的值时满足条件的整数,则输出结果为0的概率为( )
| A.0 | B.1 | C.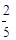 |
D.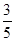 |
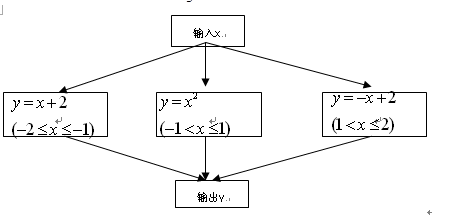
某教师的月工资数与工作的年数如下表所示(工资单位:元)
(1)填出第5年他的月工资数;
(2)用含n的代数式表示他第n年的月工资数;
(3)用(2)的代数式求该教师工作第17年的
工资数.
已知 在函数
在函数 的图象上,那么点P应在平面直角坐标系中的【 】
的图象上,那么点P应在平面直角坐标系中的【 】
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若用(1)、(2)、(3)、(4)四幅图分别表示变量之间的关系,将下面
的(a)、(b)、(c)、(d)对应的图象排序 ( )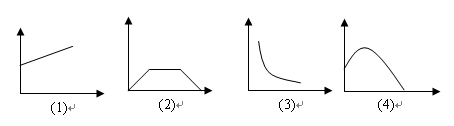
(a)面积为定值的矩形(矩形的相邻两边长的关系)
(b)运动员推出去的铅球(铅球的高度与时间的关系)
(c)一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物质量的关系)
(d)某人从A地到B地后,停留一段时间,然后按原速返回(离开A地的距离与
时间的关系)
| A.(3)(4)(1)(2) | B.(3)(2)(1)(4) |
| C.(4)(3)(1)(2) | D.(3)(4)(2)(1) |
如果函数y=(m+l)x+m2-l是正比例函数.则m的值是______________
某城市出租汽车收费标准为:4km以内(含4km)收费10元;超出4km的部分,每千米收费1.4元.写出车费y元与行驶路程x千米之间的函数关系式(x≥4)
某人乘出租汽车行驶了5km,应付多少车费?
若某人付了17元车费,那么出租车行驶了多远
由函数y=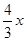 图像得到直线y=
图像得到直线y=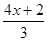 ,就是将直线y=
,就是将直线y=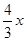 ( )
( )
| A.向上平移2个单位 | B.向右平移2个单位 |
C.向上平移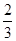 个单位 个单位 |
D.向下平移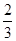 个单位 个单位 |
直线y=-x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点匀速出发,同时到达A点时运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.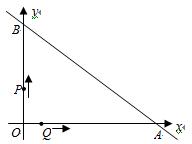
直接写出A、B两点的坐标;
设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式;
当s= 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标.
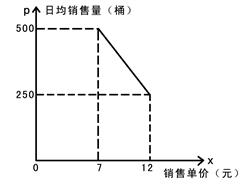
无锡市南长区某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示.求日均销售量p(桶)与销售单价x(元)的函数关系;
若该经营部希望日均获利1350元,请你根据以上信息,就该桶装水的销售单价或销售数量,提出一个用一元二次方程解决的问题,并写出解答过程.
试题篮
()