某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
观察思考
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图 ;当正方形地砖有2块时,等腰直角三角形地砖有8块(如图 ;以此类推.

规律总结
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有 为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含 的代数式表示).
问题解决
(3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢?我们可以用下面的方式来解决问题.
用点A1、A2、A3…A48分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:

(1)填写上图中第四个图中y的值为 ,第五个图中y的值为 .
(2)通过探索发现,通电话次数y与该班级人数x之间的关系式为 ,当 时,对应的y= .
(3)若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?
(阅读)
数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(理解)
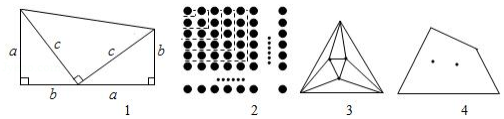
(1)如图1,两个直角边长分别为 、 、斜边长为 的直角三角形和一个两条直角边都是 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2, 行 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式: ;
(运用)
(3) 边形有 个顶点,在它的内部再画 个点,以 个点为顶点,把 边形剪成若干个三角形,设最多可以剪得 个这样的三角形.当 , 时,如图3,最多可以剪得7个这样的三角形,所以 .
①当 , 时,如图4, ;当 , 时, ;
②对于一般的情形,在 边形内画 个点,通过归纳猜想,可得 (用含 、 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.

问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是 ,纵长是 的矩形框架 、 是正整数),需要木棒的条数.
如图①,当 , 时,横放木棒为 条,纵放木棒为 条,共需4条;
如图②,当 , 时,横放木棒为 条,纵放木棒为 条,共需7条;
如图③,当 , 时,横放木棒为 条,纵放木棒为 条,共需12条;
如图④,当 , 时,横放木棒为 条,纵放木棒为 条,共需10条;
如图⑤,当 , 时,横放木棒为 条,纵放木棒为 条,共需17条.

问题(一 :当 , 时,共需木棒 条.
问题(二 :当矩形框架横长是 ,纵长是 时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是 ,纵长是 ,高是 的长方体框架 、 、 是正整数),需要木棒的条数.
如图⑥,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需46条;
如图⑦,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需75条;
如图⑧,当 , , 时,横放与纵放木棒之和为 条,竖放木棒为 条,共需104条.

问题(三 :当长方体框架的横长是 ,纵长是 ,高是 时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
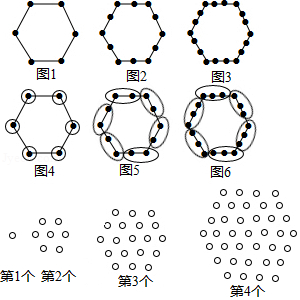
例如:图1有6个点,图2有12个点,图3有18个点, ,按此规律,求图10、图 有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是 个;图2中黑点个数是 个:图3中黑点个数是 个; ;所以容易求出图10、图 中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块,再完成以下问题:
(1)第5个点阵中有 个圆圈;第 个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
问题提出:
如图,图①是一张由三个边长为1的小正方形组成的“”形纸片,图②是一张
的方格纸
的方格纸指边长分别为
,
的矩形,被分成
个边长为1的小正方形,其中
,
,且
,
为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?
问题探究:
为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:
把图①放置在的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图③,对于的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.
探究二:
把图①放置在的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图④,在的方格纸中,共可以找到2个位置不同的
方格,依据探究一的结论可知,把图①放置在
的方格纸中,使它恰好盖住其中的三个小正方形,共有
种不同的放置方法.
探究三:
把图①放置在的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑤,在的方格纸中,共可以找到
个位置不同的
方格,依据探究一的结论可知,把图①放置在
的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.
探究四:
把图①放置在的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?
如图⑥,在的方格纸中,共可以找到 个位置不同的
方格,依据探究一的结论可知,把图①放置在
的方格纸中,使它恰好盖住其中的三个小正方形,共有 种不同的放置方法.
问题解决:
把图①放置在的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.
问题拓展:
如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为,
,
,
,
,且
,
,
是正整数)的长方体,被分成了
个棱长为1的小立方体.在图⑧的不同位置共可以找到 个图⑦这样的几何体.

(1)观察下列图形与等式的关系,并填空

(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有的代数式填空:

.
如图所示,AB=16cm,
(1)若C1是AB的中点,求AC1的长度
(2)若C2是A C1的中点,求AC2的长度
(3)若C3是A C2的中点,求AC3的长度
(4)若照上述规律发展下去,则ACn的长度是多少呢?
在数学的学习过程中,我们经常用以下的探索过程解决相关问题.
数学问题:三角形有3个顶点,如果在它的内部再画 个点,并以这
个点,并以这 个点为顶点画三角形,那么可以剪得多少个这样的三角形?
个点为顶点画三角形,那么可以剪得多少个这样的三角形?

探索规律:为了解决这个问题,我们可以从 、
、 、
、 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
(1)填表:当三角形内有4个点时,把表格补充完整;
(2)你发现的变化规律是: ;
(3)猜想:当三角形内点的个数为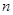 时,最多可以剪得 个三角形;
时,最多可以剪得 个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
问题解决:请你尝试用归纳的方法探索的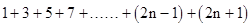 和是多少?
和是多少?
如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有1个点时,线段总共有3条,如果线段AB上有2个点时,线段总数有6条,如果线段AB上有3个点时,线段总数共有10条,…

(1)当线段AB上有6个点时,线段总数共有 条.
(2)当线段AB上有n个点时,线段总数共有 条。
(3)如果从一个多边形的一个顶点出发,分别连接这个顶点与其余各顶点,可将这个多边形分割成2003个三角形,那么此多边形的边数为多少?
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:
(1)写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示;
(2)猜想并写出与第n个图形相对应的等式.
图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n= .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
试题篮
()