如图, 中, , .以 为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 ,以 为直角边向外作等腰直角三角形 , ,连接 , , , ,分别与 , , , 交于点 , , , ,按此规律继续下去, 的面积记为 ,△ 的面积记为 ,△ 的面积记为 , ,则 .

如图,在 中, , ,若进行以下操作,在边 上从左到右依次取点 、 、 、 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ;过点 作 、 的平行线分别交 、 于点 、 ,则 .

海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.如图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第1个图至第4个图中的规律编织图案,则第5个图中有 个菱形,第 个图中有 个菱形(用含 的代数式表示).

如图,在△ 中, , ,过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ;过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ;过点 作 ,垂足为点 ,过点 作 交 于点 ,得到△ ; 按照上面的作法进行下去,则△ 的面积为 .(用含正整数 的代数式表示)

如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 .连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

如图,每个图案都由大小相同的正方形组成,按照此规律,第 个图案中这样的正方形的总个数可用含 的代数式表示为 .

下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒, ,按此规律,图案⑦需 根火柴棒.

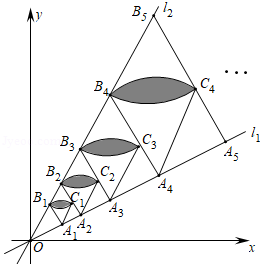
如图,直线 的解析式是 ,直线 的解析式是 ,点 在 上, 的横坐标为 ,作 交 于点 ,点 在 上,以 , 为邻边在直线 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 ;延长 交 于点 ,点 在 上,以 , 为邻边在 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 按照此规律继续作下去,则 .(用含有正整数 的式子表示)
将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆 按此规律排列下去,则前50行共有圆 个.

如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; , 的圆心依次按点 , , , 循环.若正方形 的边长为1,则 的长是 .

庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言) .

图2也是一种无限分割:在 中, , ,过点 作 于点 ,再过点 作 于点 ,又过点 作 于点 ,如此无限继续下去,则可将利 分割成 、△ 、△ 、△ 、 、△ 、 .假设 ,这些三角形的面积和可以得到一个等式是 .
试题篮
()