初中数学规律型：图形的变化类填空题

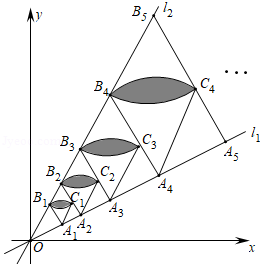
如图，由两个长为2，宽为1的长方形组成“7”字图形

（1）将一个“7”字图形按如图摆放在平面直角坐标系中，记为“7”字图形，其中顶点位于轴上，顶点，位于轴上，为坐标原点，则的值为　　．

（2）在（1）的基础上，继续摆放第二个“7”字图形得顶点，摆放第三个“7”字图形得顶点，依此类推，，摆放第个“7”字图形得顶点，，则顶点的坐标为　　．

如图，四边形 $\mathit{OA}{A}_1{B}_1$是边长为1的正方形，以对角线 $O{A}_1$为边作第二个正方形 $O{A}_1{A}_2{B}_2$．连接 $A{A}_2$，得到△ $A{A}_1{A}_2$；再以对角线 $O{A}_2$为边作第三个正方形 $O{A}_2{A}_3{B}_3$，连接 $A_1{A}_3$，得到△ $A_1{A}_2{A}_3$；再以对角线 $O{A}_3$为边作第四个正方形，连接 $A_2{A}_4$，得到△ $A_2{A}_3{A}_4\dots \dots$记△ $A{A}_1{A}_2$、△ $A_1{A}_2{A}_3$、△ $A_2{A}_3{A}_4$的面积分别为 $S_1$、 $S_2$、 $S_3$，如此下去，则 $S_n=$　　．

下列图形是用围棋子按一定规律摆放的，根据摆放规律，第20个图中围棋子的个数是　　．

如图，每个图案都由大小相同的正方形组成，按照此规律，第 $n$个图案中这样的正方形的总个数可用含 $n$的代数式表示为　       　．

如图，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第五个图形需要黑色棋子的个数是      ，第n个图形需要黑色棋子的个数是      （n≥1，且n为整数）．

下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒， $\dots$，按此规律，图案⑦需　　根火柴棒．

如图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第（是正整数)个图案中由                个基础图形组成．
 

如图，直线 $l_1$的解析式是 $y=\frac{\sqrt{3}}{3}x$，直线 $l_2$的解析式是 $y=\sqrt{3}x$，点 $A_1$在 $l_1$上， $A_1$的横坐标为 $\frac{3}{2}$，作 $A_1{B}_1\perp l_1$交 $l_2$于点 $B_1$，点 $B_2$在 $l_2$上，以 $B_1{A}_1$， $B_1{B}_2$为邻边在直线 $l_1$， $l_2$间作菱形 $A_1{B}_1{B}_2{C}_1$，分别以点 $A_1$， $B_2$为圆心，以 $A_1{B}_1$为半径画弧得扇形 $B_1{A}_1{C}_1$和扇形 $B_1{B}_2{C}_1$，记扇形 $B_1{A}_1{C}_1$与扇形 $B_1{B}_2{C}_1$重叠部分的面积为 $S_1$；延长 $B_2{C}_1$交 $l_1$于点 $A_2$，点 $B_3$在 $l_2$上，以 $B_2{A}_2$， $B_2{B}_3$为邻边在 $l_1$， $l_2$间作菱形 $A_2{B}_2{B}_3{C}_2$，分别以点 $A_2$， $B_3$为圆心，以 $A_2{B}_2$为半径画弧得扇形 $B_2{A}_2{C}_2$和扇形 $B_2{B}_3{C}_2$，记扇形 $B_2{A}_2{C}_2$与扇形 $B_2{B}_3{C}_2$重叠部分的面积为 $S_2\dots \dots \dots$按照此规律继续作下去，则 $S_n=$　　．（用含有正整数 $n$的式子表示）

将一些圆按照如图方式摆放，从上向下有无数行，其中第一行有2个圆，第二行有4个圆，第三行有6个圆 $\dots$按此规律排列下去，则前50行共有圆　　个．

下面图形都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第   

　　个图形共有210个小球．

如图，四边形 $\mathit{ABCD}$是正方形，曲线 $D{A}_1{B}_1{C}_1{D}_1{A}_2\dots$是由一段段90度的弧组成的．其中： $\stackrel{̂}{D{A}_1}$的圆心为点 $A$，半径为 $\mathit{AD}$； $\stackrel{̂}{A_1{B}_1}$的圆心为点 $B$，半径为 $B{A}_1$； $\stackrel{̂}{B_1{C}_1}$的圆心为点 $C$，半径为 $C{B}_1$； $\stackrel{̂}{C_1{D}_1}$的圆心为点 $D$，半径为 $D{C}_1$； $\dots \stackrel{̂}{D{A}_1},\stackrel{̂}{A_1{B}_1},\stackrel{̂}{B_1{C}_1},\stackrel{̂}{C_1{D}_1}$， $\dots$的圆心依次按点 $A$， $B$， $C$， $D$循环．若正方形 $\mathit{ABCD}$的边长为1，则 $\stackrel{̂}{A_{2020}{B}_{2020}}$的长是　　．

如图，用同样大小的黑色棋子按如图所示的规律摆放：则第⑦个图案有　　个黑色棋子．

庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言） $:1=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\dots +\frac{1}{2^n}+\dots$．

图2也是一种无限分割：在 $\mathit{\Delta ABC}$中， $\angle C=90°$， $\angle B=30°$，过点 $C$作 $C{C}_1\perp \mathit{AB}$于点 $C_1$，再过点 $C_1$作 $C_1{C}_2\perp \mathit{BC}$于点 $C_2$，又过点 $C_2$作 $C_2{C}_3\perp \mathit{AB}$于点 $C_3$，如此无限继续下去，则可将利 $\mathit{\Delta ABC}$分割成 $\mathit{\Delta AC}{C}_1$、△ $C{C}_1{C}_2$、△ $C_1{C}_2{C}_3$、△ $C_2{C}_3{C}_4$、 $\dots$、△ $C_{n-2}{C}_{n-1}{C}_n$、 $\dots$．假设 $\mathit{AC}=2$，这些三角形的面积和可以得到一个等式是　　．

如图，边长为1的正三角形 $\mathit{ABC}$放置在边长为2的正方形内部，顶点 $A$在正方形的一个顶点上，边 $\mathit{AB}$在正方形的一边上，将 $\mathit{\Delta ABC}$绕点 $B$顺时针旋转，当点 $C$落在正方形的边上时，完成第1次无滑动滚动（如图 $1)$；再将 $\mathit{\Delta ABC}$绕点 $C$顺时针旋转，当点 $A$落在正方形的边上时，完成第2次无滑动滚动（如图 $2)$， $\dots$，每次旋转的角度都不大于 $120°$，依次这样操作下去，当完成第2016次无滑动滚动时，点 $A$经过的路径总长为　　．

用m根火柴棒恰好可拼成如图1所示的a个等边三角形或如图2所示的b个正六边形，则 $\frac{b}{a}$＝　　．