初中数学完全平方公式试题

已知是一个完全式，则k的值是（ ）

A．8

B．±8

C．16

D．±16

下列运算正确的是（  ）

A．

B．

C．

D．

先阅读理解下面的例题，再按要求解答下列问题：
例题 ：求代数式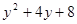的最小值．
解：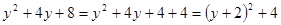
  
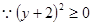
的最小值是．
（1）代数式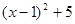的最小值         ；
（2）求代数式的最小值；
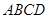（3）某居民小区要在一块一边靠墙（墙长）的空地上建一个长方形花园，花园一边靠墙，另三边用总长为的栅栏围成．如图，设（），请问:当取何值时，花园的面积最大？最大面积是多少？

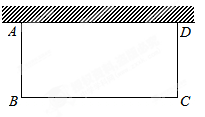
图1是一个长为2，宽为2的长方形，沿图中虚线剪开，可分成四块小长方形．

（1）求出图1的长方形面积；
（2）将四块小长方形拼成一个图2的正方形．利用阴影部分面积的不同表示方法，直接写出代数式（）²、（）²、之间的等量关系；
（3）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用阴影表示．求两块阴影部分的周长和（用含、的代数式表示）．

若，．求：
（1）的值；
（2）的值．

图①是一个长为、宽为的长方形，用这样四个全等的长方形，拼成如图②的正方形．

（1）按要求填空：
ⅰ．请用含字母、的代数式表示图②中的阴影部分的正方形的边长：              ；
ⅱ．请用含字母、的代数式，用两种不同的方法表示图②中阴影部分的面积：
方法1：                     
方法2：                     
ⅲ．观察图②，请写出代数式、、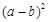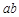之间的等量关系：                  ；
（2）根据（1）题中的等量关系，解决如下问题：
若，，求的值．

若多项式是一个完全平方式，则实数的值为              ．

已知 （1）求的值。（2）求的值。

小马虎在下面的计算中只做对了一道题，他做对的题目是（   ）

A．	B．
C．	D．

若是完全平方式，则k的值是（     ）

A．2

B．±2

C．±4

D．4

若的值是（    ）

A．1

B．25

C．2

D．-10

（1）拼一拼，画一画：请你用4个长为a，宽为b的矩形拼成一个大正方形，并且正中间留下一个洞，这个洞恰好是一个小正方形．
（2）计算中间的小正方形的面积，聪明的你能发现什么？
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长．

若a²﹣4a+b²﹣10b+29=0，求a²b+ab²的值．

已知4x²＋mx＋9是完全平方式，则m＝_________．

已知（a+b）²=7，（a﹣b）²=4，则ab的值为            ．