如图①,四边形 中, , , 从 点出发,以每秒1个单位长度的速度,按 的顺序在边上匀速运动,设 点的运动时间为 秒, 的面积为 , 关于 的函数图象如图②所示,当 运动到 中点时, 的面积为 .
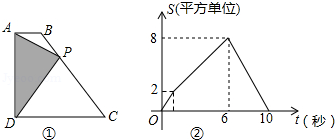
如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为 ,两个三角形重叠面积为 ,则 关于 的函数图象是
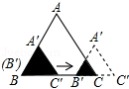
A.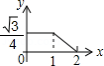 B.
B.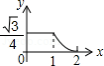
C. D.
D.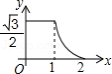
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形 如图乙所示, 米, 米,在五边形 区域上种植花卉,则大正方形花坛种植花卉的面积 与 的函数图象大致是

A. B.
B.
C. D.
D.
如图, 为等边三角形,点 从 出发,沿 作匀速运动,则线段 的长度 与运动时间 之间的函数关系大致是

A. B.
B.
C. D.
D.
已知点 为某个封闭图形边界上一定点,动点 从点 出发,沿其边界顺时针匀速运动一周,设点 的运动时间为 ,线段 的长度为 ,表示 与 的函数图象大致如图所示,则该封闭图形可能是

A.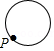 B.
B.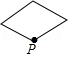 C.
C.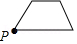 D.
D.
如图①,在矩形 中, ,对角线 , 相交于点 ,动点 由点 出发,沿 向点 运动.设点 的运动路程为 , 的面积为 , 与 的函数关系图象如图②所示,则 边的长为
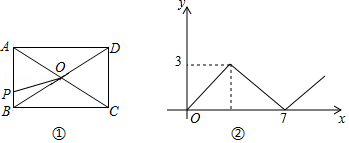
A.3B.4C.5D.6
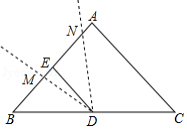
如图,在 中, , ,点 为 的中点, ,将 绕点 顺时针旋转 度 ,角的两边分别交直线 于 、 两点,设 、 两点间的距离为 , , 两点间的距离为 .
小涛根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是 , 两点间的距离 进行取点、画图、测量,分别得到了 与 的几组对应值:
|
0 |
0.30 |
0.50 |
1.00 |
1.50 |
2.00 |
2.50 |
|
3.00 |
3.50 |
3.68 |
3.81 |
3.90 |
3.93 |
4.10 |
|
|
2.88 |
2.81 |
2.69 |
2.67 |
2.80 |
3.15 |
|
3.85 |
5.24 |
6.01 |
6.71 |
7.27 |
7.44 |
8.87 |
请你通过计算,补全表格;
(2)描点、连线,在平面直角坐标系 中,描出表格中各组数值所对应的点 ,并画出函数 关于 的图象.

(3)探究性质:随着自变量 的不断增大,函数 的变化趋势: .
(4)解决问题:当 时, 的长度大约是 .(保留两位小数).
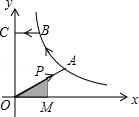
如图,已知A,B是反比例函数 图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿 (图中“→”所示路线)匀速运动,终点为C,过P作 轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A.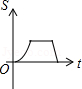 B.
B.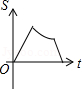
C.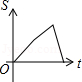 D.
D.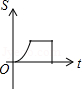
如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )

A. B.
B.
C.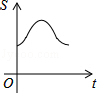 D.
D.
如图,在等腰△ABC中, , ,点P从点B出发,以 的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿 方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )

A. B.
B.
C. D.
D.
如图①,在边长为4cm的正方形ABCD中,点P以每秒2cm的速度从点A出发,沿AB→BC的路径运动,到点C停止.过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动2.5秒时,PQ的长是( )

A.2 cmB.3 cmC.4 cmD.5 cm
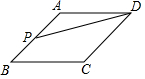
如图,点 P是菱形 ABCD边上的一动点,它从点 A出发沿在 A→ B→ C→ D路径匀速运动到点 D,设△ PAD的面积为 y, P点的运动时间为 x,则 y关于 x的函数图象大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
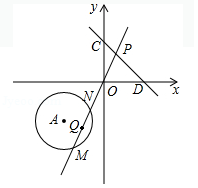
如图,直线 y=﹣ x+4与 x轴、 y轴分别交于 D, C两点, P是直线 CD上的一个动点,⊙ A的圆心 A的坐标为(﹣4,﹣4),半径为2 ,直线 PO与⊙ A相交于 M, N两点, Q是 MN的中点.当 OP= t, OQ= S,则 S与 t的函数图象大致为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )

A. B.
B.
C. D.
D.
试题篮
()