如图,矩形 中, , ,点 从点 出发,以 的速度沿 方向匀速运动,同时点 从点 出发,以 的速度沿 方向匀速运动,当一个点到达点 时,另一个点也随之停止.设运动时间为 , 的面积为 ,下列能大致反映 与 之间函数关系的图象是

A.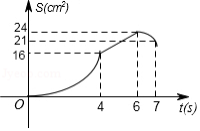
B.
C.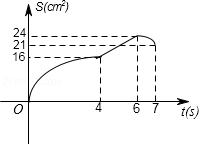
D.
如图,菱形 的边长是4厘米, ,动点 以1厘米秒的速度自 点出发沿 方向运动至 点停止,动点 以2厘米 秒的速度自 点出发沿折线 运动至 点停止.若点 、 同时出发运动了 秒,记 的面积为 厘米 ,下面图象中能表示 与 之间的函数关系的是
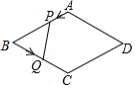
A.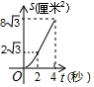 B.
B.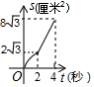
C.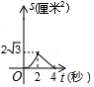 D.
D.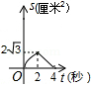
如图,在 中, , , ,矩形 中 , ,点 和点 重合,点 、 、 在同一直线上,令 不动,矩形 沿 所在直线以每秒 的速度向右移动,至点 与点 重合为止,设移动 秒后,矩形 与 重叠部分的面积为 ,则 与 的大致图象是

A. B.
B.
C. D.
D.
如图,已知矩形 中, , .动点 在边 上从点 向 运动,速度为 ;同时动点 从点 出发,沿折线 运动,速度为 .当一个点到达终点时,另一个点随之停止运动.设点 运动的时间为 , 的面积为 ,则描述 与时间 的函数关系的图象大致是
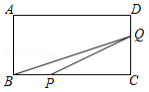
A.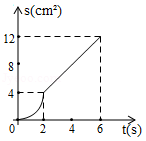 B.
B.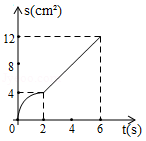
C.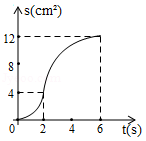 D.
D.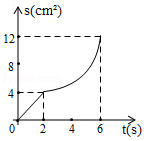
如图,在 中,点 是 的内心,连接 , ,过点 作 分别交 , 于点 , .已知 的周长为8, , 的周长为 ,则表示 与 的函数图象大致是
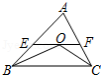
A.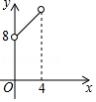 B.
B.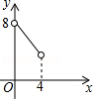
C.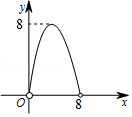 D.
D.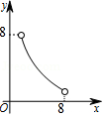
已知,等边三角形 和正方形 的边长相等,按如图所示的位置摆放 点与 点重合),点 、 、 共线, 沿 方向匀速运动,直到 点与 点重合.设运动时间为 ,运动过程中两图形重叠部分的面积为 ,则下面能大致反映 与 之间关系的函数图象是

A. B.
B.
C. D.
D.
如图①,在矩形 中, 是 上一点,点 从点 沿折线 运动到点 时停止;点 从点 沿 运动到点 时停止,速度均为每秒1个单位长度.如果点 、 同时开始运动,设运动时间为 , 的面积为 ,已知 与 的函数图象如图②所示,以下结论:① ;② ;③当 时, ;④当 时, 是等腰三角形;⑤当 时, ,其中正确的有

A.2个B.3个C.4个D.5个
如图,边长为4个单位长度的正方形 的边 与等腰直角三角形 的斜边 重合, 以每秒1个单位长度的速度沿 向右匀速运动(保持 ,当点 运动到 边上时 停止运动,设 的运动时间为 秒, 与正方形 重叠部分的面积为 ,则 关于 的函数大致图象为

A. B.
B.
C. D.
D.
如图, 、 、 、 为圆 的四等分点,动点 从圆心 出发,沿 的路线做匀速运动,当点 运动到圆心 时立即停止,设运动时间为 , 的度数为 度,则下列图象中表示 (度 与 之间的函数关系最恰当的是
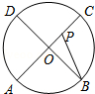
A.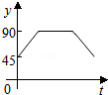 B.
B.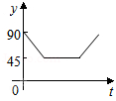
C.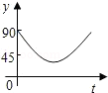 D.
D.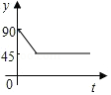
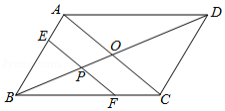
如图,平行四边形 中,对角线 、 相交于点 ,且 , , 是对角线 上任意一点,过点 作 ,与平行四边形的两条边分别交于点 、 .设 , ,则能大致表示 与 之间关系的图象为
A.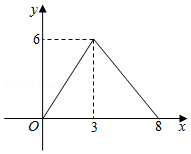
B.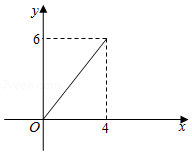
C.
D.
如图,在矩形 中,点 从点 出发,沿着矩形的边顺时针方向运动一周回到点 ,则点 、 、 围成的图形面积 与点 运动路程 之间形成的函数关系式的大致图象是

A.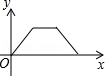 B.
B.
C. D.
D.
如图,在正方形 中, ,动点 自 点出发沿 方向以每秒 的速度运动,同时动点 自 点出发沿折线 以每秒 的速度运动,到达 点时运动同时停止,设 的面积为 ,运动时间为 (秒 ,则下列图象中能大致反映 与 之间函数关系的是

A.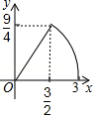 B.
B.
C. D.
D.
如图,在边长为2的正方形 中剪去一个边长为1的小正方形 ,动点 从点 出发,沿 的路线绕多边形的边匀速运动到点 时停止(不含点 和点 ,则 的面积 随着时间 变化的函数图象大致是

A. B.
B. C.
C. D.
D.
如图,点 的坐标为 ,点 是 轴正半轴上的一动点,以 为边作等腰直角 ,使 ,设点 的横坐标为 ,点 的纵坐标为 ,能表示 与 的函数关系的图象大致是
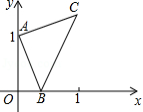
A. B.
B.
C. D.
D.
试题篮
()