初中数学一次函数的应用解答题

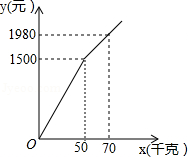
受新冠肺炎疫情影响，一水果种植专业户有大量成熟水果无法出售．"一方有难，八方支援"某水果经销商主动从该种植专业户购进甲，乙两种水果进行销售．专业户为了感谢经销商的援助，对甲种水果的出售价格根据购买量给予优惠，对乙种水果按25元 $/$ 千克的价格出售．设经销商购进甲种水果 $x$ 千克，付款 $y$ 元， $y$ 与 $x$ 之间的函数关系如图所示．

（1）直接写出当 $0⩽x⩽50$ 和 $x>50$ 时， $y$ 与 $x$ 之间的函数关系式；

（2）若经销商计划一次性购进甲，乙两种水果共100千克，且甲种水果不少于40千克，但又不超过60千克．如何分配甲，乙两种水果的购进量，才能使经销商付款总金额 $w$ （元 $)$ 最少？

（3）若甲，乙两种水果的销售价格分别为40元 $/$ 千克和36元 $/$ 千克．经销商按（2）中甲，乙两种水果购进量的分配比例购进两种水果共 $a$ 千克，且销售完 $a$ 千克水果获得的利润不少于1650元，求 $a$ 的最小值．

某食品连锁店研制出一种新式月饼，每块成本为6元．试销一段时间后发现，若每块月饼的售价不超过10元，每天可销售300块；若每块月饼的售价超过10元，每提高1元，每天的销量就会减少30块．这家食品连锁店每天需要支付因生产这种月饼而产生的其他费用（不含月饼成本）200元．设每块月饼的售价为 $x$（元 $)$，食品连锁店每天销售这种月饼的纯收入为 $y$（元 $)$．（注：纯收入 $=$销售额 $-$成本 $-$其他费用）

（1）当每块月饼售价不超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　．当每块月饼售价超过10元时，请直接写出 $y$与 $x$之间的函数关系式：　　；

（2）如果这种月饼每块的售价不超过12元，那么如何定价才能使该食品连锁店每天销售这种月饼的纯收入提高？最高纯收入为多少元？

某公司分别在 $A$ ， $B$ 两城生产同种产品，共100件． $A$ 城生产产品的总成本 $y$ （万元）与产品数量 $x$ （件 $)$ 之间具有函数关系 $y=a{x}^2+\mathit{bx}$ ．当 $x=10$ 时， $y=400$ ；当 $x=20$ 时， $y=1000$ ． $B$ 城生产产品的每件成本为70万元．

（1）求 $a$ ， $b$ 的值；

（2）当 $A$ ， $B$ 两城生产这批产品的总成本的和最少时，求 $A$ ， $B$ 两城各生产多少件？

（3）从 $A$ 城把该产品运往 $C$ ， $D$ 两地的费用分别为 $m$ 万元 $/$ 件和3万元 $/$ 件；从 $B$ 城把该产品运往 $C$ ， $D$ 两地的费用分别为1万元 $/$ 件和2万元 $/$ 件． $C$ 地需要90件， $D$ 地需要10件，在（2）的条件下，直接写出 $A$ ， $B$ 两城总运费的和的最小值（用含有 $m$ 的式子表示）．

某通讯公司就手机流量套餐推出三种方案，如下表：

	$A$ 方案	$B$ 方案	$C$ 方案
每月基本费用（元     $)$	20	56	266
每月免费使用流量（兆     $)$	1024	$m$	无限
超出后每兆收费（元     $)$	$n$	$n$

$A$ ， $B$ ， $C$ 三种方案每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系如图所示．

（1）请写出 $m$ ， $n$ 的值．

（2）在 $A$ 方案中，当每月使用的流量不少于1024兆时，求每月所需的费用 $y$ （元 $)$ 与每月使用的流量 $x$ （兆 $)$ 之间的函数关系式．

（3）在这三种方案中，当每月使用的流量超过多少兆时，选择 $C$ 方案最划算？

为了抗击新冠疫情，我市甲、乙两厂积极生产了某种防疫物资共500吨，乙厂的生产量是甲厂的2倍少100吨．这批防疫物资将运往 $A$ 地240吨， $B$ 地260吨，运费如下表（单位：元 $/$ 吨）．

目的地 生产厂	$A$	$B$
甲	20	25
乙	15	24

（1）求甲、乙两厂各生产了这批防疫物资多少吨？

（2）设这批物资从乙厂运往 $A$ 地 $x$ 吨，全部运往 $A$ ， $B$ 两地的总运费为 $y$ 元．求 $y$ 与 $x$ 之间的函数关系式，并设计使总运费最少的调运方案；

（3）当每吨运费均降低 $m$ 元 $(0<m⩽15$ 且 $m$ 为整数）时，按（2）中设计的调运方案运输，总运费不超过5200元．求 $m$ 的最小值．

某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量 $y$（本 $)$与每本纪念册的售价 $x$（元 $)$之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

（1）请直接写出 $y$与 $x$的函数关系式；

（2）当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

（3）设该文具店每周销售这种纪念册所获得的利润为 $w$元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

某校足球队需购买 $A$ 、 $B$ 两种品牌的足球．已知 $A$ 品牌足球的单价比 $B$ 品牌足球的单价高20元，且用900元购买 $A$ 品牌足球的数量用720元购买 $B$ 品牌足球的数量相等．

（1）求 $A$ 、 $B$ 两种品牌足球的单价；

（2）若足球队计划购买 $A$ 、 $B$ 两种品牌的足球共90个，且 $A$ 品牌足球的数量不小于 $B$ 品牌足球数量的2倍，购买两种品牌足球的总费用不超过8500元．设购买 $A$ 品牌足球 $m$ 个，总费用为 $W$ 元，则该队共有几种购买方案？采用哪一种购买方案可使总费用最低？最低费用是多少元？

某销售商准备在南充采购一批丝绸，经调查，用10000元采购 $A$型丝绸的件数与用8000元采购 $B$型丝绸的件数相等，一件 $A$型丝绸进价比一件 $B$型丝绸进价多100元．

（1）求一件 $A$型、 $B$型丝绸的进价分别为多少元？

（2）若销售商购进 $A$型、 $B$型丝绸共50件，其中 $A$型的件数不大于 $B$型的件数，且不少于16件，设购进 $A$型丝绸 $m$件．

①求 $m$的取值范围．

②已知 $A$型的售价是800元 $/$件，销售成本为 $2n$元 $/$件； $B$型的售价为600元 $/$件，销售成本为 $n$元 $/$件．如果 $50⩽n⩽150$，求销售这批丝绸的最大利润 $w$（元 $)$与 $n$（元 $)$的函数关系式（每件销售利润 $=$售价 $-$进价 $-$销售成本）．

Ⅰ号无人机从海拔 $10m$ 处出发，以 $10m/\mathit{min}$ 的速度匀速上升，Ⅱ号无人机从海拔 $30m$ 处同时出发，以 $a(m/\mathit{min})$ 的速度匀速上升，经过 $5\mathit{min}$ 两架无人机位于同一海拔高度 $b\left(m\right)$ ．无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系如图．两架无人机都上升了 $15\mathit{min}$ ．

（1）求 $b$ 的值及Ⅱ号无人机海拔高度 $y\left(m\right)$ 与时间 $x\left(\mathit{min}\right)$ 的关系式；

（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

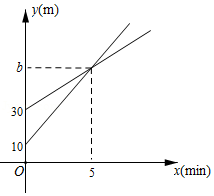
李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程 $s$ （千米）与行驶时间 $t$ （小时）的关系如图所示（中途休息、加油的时间不计）．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升 $/$ 千米，请根据图象解答下列问题：

（1）写出工厂离目的地的路程；

（2）求 $s$ 关于 $t$ 的函数表达式；

（3）当货车显示加油提醒后，问行驶时间 $t$ 在怎样的范围内货车应进站加油？

国庆节前，某超市为了满足人们的购物需求，计划购进甲、乙两种水果进行销售．经了解，甲种水果和乙种水果的进价与售价如下表所示．

	甲	乙
进价（元/千克）	x	x+4
售价（元/千克）	20	25

已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同．

（1）求x的值；

（2）若超市购进这两种水果共100千克，其中甲种水果的重量不低于乙种水果重量的3倍，则超市应如何进货才能获得最大利润，最大利润是多少？

疫苗接种，利国利民．甲、乙两地分别对本地各40万人接种新冠疫苗．甲地在前期完成5万人接种后，甲、乙两地同时以相同速度接种，甲地经过 $a$ 天后接种人数达到25万人，由于情况变化，接种速度放缓，结果100天完成接种任务，乙地80天完成接种任务，在某段时间内，甲、乙两地的接种人数 $y$ （万人）与各自接种时间 $x$ （天 $)$ 之间的关系如图所示．

（1）直接写出乙地每天接种的人数及 $a$ 的值；

（2）当甲地接种速度放缓后，求 $y$ 关于 $x$ 的函数解析式，并写出自变量 $x$ 的取值范围；

（3）当乙地完成接种任务时，求甲地未接种疫苗的人数．

某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗早期在农科所的温室中生长，长到大约 $20\mathit{cm}$时，移至该村的大棚内，沿插杆继续向上生长．研究表明，60天内，这种瓜苗生长的高度 $y\left(\mathit{cm}\right)$与生长时间 $x$（天 $)$之间的关系大致如图所示．

（1）求 $y$与 $x$之间的函数关系式；

（2）当这种瓜苗长到大约 $80\mathit{cm}$时，开始开花结果，试求这种瓜苗移至大棚后．继续生长大约多少天，开始开花结果？

某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品 $x$（吨），生产甲、乙两种产品获得的总利润为 $y$（万元）．

（1）求 $y$与 $x$之间的函数表达式；

（2）若每生产1吨甲产品需要 $A$原料0.25吨，每生产1吨乙产品需要 $A$原料0.5吨．受市场影响，该厂能获得的 $A$原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

我州某养殖场计划购买甲、乙两种鱼苗600条，甲种鱼苗每条16元，乙种鱼苗每条20元，相关资料表明：甲、乙两种鱼苗的成活率为 $80\%$， $90\%$

（1）若购买这两种鱼苗共用去11000元，则甲、乙两种鱼苗各购买多少条？

（2）若要使这批鱼苗的总成活率不低于 $85\%$，则乙种鱼苗至少购买多少条？

（3）在（2）的条件下，应如何选购鱼苗，使购买鱼苗的总费用最低？最低费用是多少？