某通讯公司就手机流量套餐推出三种方案,如下表:
| |
方案 |
方案 |
方案 |
| 每月基本费用(元 |
20 |
56 |
266 |
| 每月免费使用流量(兆 |
1024 |
|
无限 |
| 超出后每兆收费(元 |
|
|
|
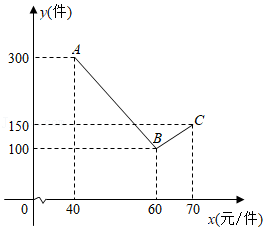
, , 三种方案每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系如图所示.
(1)请写出 , 的值.
(2)在 方案中,当每月使用的流量不少于1024兆时,求每月所需的费用 (元 与每月使用的流量 (兆 之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择 方案最划算?

某地区山峰的高度每增加1百米,气温大约降低 ,气温 和高度 (百米)的函数关系如图所示.
请根据图象解决下列问题:
(1)求高度为5百米时的气温;
(2)求 关于 的函数表达式;
(3)测得山顶的气温为 ,求该山峰的高度.

在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.

已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍.给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(Ⅰ)填表:
离开宿舍的时间 |
2 |
5 |
20 |
23 |
30 |
离宿舍的距离 |
0.2 |
0.5 |
0.7 |
|
|
(Ⅱ)填空:
①食堂到图书馆的距离为 ;
②小亮从食堂到图书馆的速度为 ;
③小亮从图书馆返回宿舍的速度为 ;
④当小亮离宿舍的距离为 时,他离开宿舍的时间为 .
(Ⅲ)当 时,请直接写出 关于 的函数解析式.
某商家正在热销一种商品,其成本为30元 件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元 件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量 (件 与售价 (元 件)满足如图所示的函数关系(其中 ,且 为整数).
(1)写出 与 的函数关系式;
(2)当售价为多少时,商家所获利润最大,最大利润是多少?
我国传统的计重工具 秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为 (厘米)时,秤钩所挂物重为 (斤 ,则 是 的一次函数.下表中为若干次称重时所记录的一些数据.
(厘米) |
1 |
2 |
4 |
7 |
11 |
12 |
(斤 |
0.75 |
1.00 |
1.50 |
2.75 |
3.25 |
3.50 |
(1)在上表 , 的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?

2020年5月16日,“钱塘江诗路”航道全线开通.一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为 ,游轮行驶的时间记为 ,两艘轮船距离杭州的路程 关于 的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中 点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距 ?

(2)①求出 , , , 的坐标,利用待定系数法求解即可.
②分三种情形种情形分别构建方程求解即可.
李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 (千米)与行驶时间 (小时)的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升 千米,请根据图象解答下列问题:
(1)写出工厂离目的地的路程;
(2)求 关于 的函数表达式;
(3)当货车显示加油提醒后,问行驶时间 在怎样的范围内货车应进站加油?

今年植树节期间,某景观园林公司购进一批成捆的 , 两种树苗,每捆 种树苗比每捆 种树苗多10棵,每捆 种树苗和每捆 种树苗的价格分别是630元和600元,而每棵 种树苗和每棵 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵, 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进 种树苗和 种树苗各多少棵?并求出最低费用.
新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店三月份共销售 , 两种型号的口罩9000只,共获利润5000元,其中 , 两种型号口罩所获利润之比为 .已知每只 型口罩的销售利润是 型口罩的1.2倍.
(1)求每只 型口罩和 型口罩的销售利润;
(2)该药店四月份计划一次性购进两种型号的口罩共10000只,其中 型口罩的进货量不超过 型口罩的1.5倍,设购进 型口罩 只,这10000只口罩的销售总利润为 元.该药店如何进货,才能使销售总利润最大?
, 两地相距 ,甲货车从 地以 的速度匀速前往 地,到达 地后停止.在甲出发的同时,乙货车从 地沿同一公路匀速前往 地,到达 地后停止.两车之间的路程 与甲货车出发时间 之间的函数关系如图中的折线 所示.其中点 的坐标是 ,点 的坐标是 ,则点 的坐标是 .

, 两地相距200千米.早上 货车甲从 地出发将一批物资运往 地,行驶一段路程后出现故障,即刻停车与 地联系. 地收到消息后立即派货车乙从 地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往 地.两辆货车离开各自出发地的路程 (千米)与时间 (小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程 关于 的函数表达式.
(2)因实际需要,要求货车乙到达 地的时间比货车甲按原来的速度正常到达 地的时间最多晚1个小时,问货车乙返回 地的速度至少为每小时多少千米?

国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示.
甲 |
乙 |
|
进价(元/千克) |
x |
x+4 |
售价(元/千克) |
20 |
25 |
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)求x的值;
(2)若超市购进这两种水果共100千克,其中甲种水果的重量不低于乙种水果重量的3倍,则超市应如何进货才能获得最大利润,最大利润是多少?
甲、乙两人沿同一直道从 地去 地.甲比乙早 出发,乙的速度是甲的2倍.在整个行程中,甲离 地的距离 (单位: 与时间 (单位: 之间的函数关系如图所示.
(1)在图中画出乙离 地的距离 (单位: 与时间 之间的函数图象;
(2)若甲比乙晚 到达 地,求甲整个行程所用的时间.

渠县是全国优质黄花主产地,某加工厂加工黄花的成本为30元 千克,根据市场调查发现,批发价定为48元 千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
(1)写出工厂每天的利润 元与降价 元之间的函数关系.当降价2元时,工厂每天的利润为多少元?
(2)当降价多少元时,工厂每天的利润最大,最大为多少元?
(3)若工厂每天的利润要达到9750元,并让利于民,则定价应为多少元?
试题篮
()