如图,在平面直角坐标系中,抛物线 经过点 和 .
(1)求抛物线 的对称轴.
(2)当 时,将抛物线 向左平移2个单位,再向下平移1个单位,得到抛物线 .
①求抛物线 的解析式.
②设抛物线 与 轴交于 , 两点(点 在点 的右侧),与 轴交于点 ,连接 .点 为第一象限内抛物线 上一动点,过点 作 于点 .设点 的横坐标为 .是否存在点 ,使得以点 , , 为顶点的三角形与 相似,若存在,求出 的值;若不存在,请说明理由.

如图,在平面直角坐标系 中,平行四边形 的 边与 轴交于 点, 是 的中点, 、 、 的坐标分别为 , , .
(1)求过 、 、 三点的抛物线的解析式;
(2)试判断抛物线的顶点是否在直线 上;
(3)设过 与 平行的直线交 轴于 , 是线段 之间的动点,射线 与抛物线交于另一点 ,当 的面积最大时,求 的坐标.
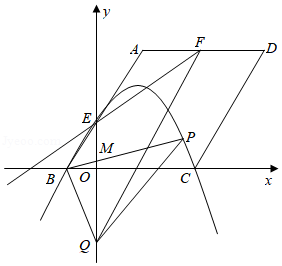
甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 ,桥拱顶点 到水面的距离是 .
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为 的打捞船径直向桥驶来,当船驶到桥拱下方且距 点 时,桥下水位刚好在 处,有一名身高 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平).
(3)如图③,桥拱所在的函数图象是抛物线 ,该抛物线在 轴下方部分与桥拱 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 个单位长度,平移后的函数图象在 时, 的值随 值的增大而减小,结合函数图象,求 的取值范围.
如图,已知抛物线 与 轴相交于 , 两点,与 轴相交于点 ,对称轴是直线 ,连接 .
(1)求该抛物线的表达式;
(2)若过点 的直线 与抛物线相交于另一点 ,当 时,求直线 的表达式;
(3)在(2)的条件下,当点 在 轴下方时,连接 ,此时在 轴左侧的抛物线上存在点 ,使 .请直接出所有符合条件的点 的坐标.

如图(1),在平面直角坐标系中,抛物线 与y轴交于点A,与x轴交于点 ,且经过点B(8,4),连接AB,BO,作 于点M,将 沿y轴翻折,点M的对应点为点N.解答下列问题:
(1)抛物线的解析式为 ,顶点坐标为 ;
(2)判断点N是否在直线AC上,并说明理由;
(3)如图(2),将图(1)中 沿着OB平移后,得到 .若DE边在线段OB上,点F在抛物线上,连接AF,求四边形 的面积.

如图,二次函数 的图象过点 , ,交y轴于点 .直线BO与抛物线相交于另一点D,连接 ,点E是线段AB上的一动点,过点E作 交AD于点F.
(1)求二次函数 的表达式;
(2)判断 的形状,并说明理由;
(3)在点E的运动过程中,直线 上存在一点G,使得四边形AFGE为矩形,请判断此时 的数量关系,并求出点E的坐标;
(4)点H是抛物线的顶点,在(3)的条件下,点P是平面内使得 的点,在抛物线的对称轴上,是否存在点Q,使得 是以 为直角的等腰直角三角形,若存在,直接写出符合条件的所有点Q的坐标;若不存在,请说明理由.

如图,在直角坐标系中,四边形 是平行四边形,经过 , , 三点的抛物线 与 轴的另一个交点为 ,其顶点为 ,对称轴与 轴交于点 .
(1)求这条抛物线对应的函数表达式;
(2)已知 是抛物线上的点,使得 的面积是 的面积的 ,求点 的坐标;
(3)已知 是抛物线对称轴上的点,满足在直线 上存在唯一的点 ,使得 ,求点 的坐标.

如图,抛物线 交 轴于 , 两点,与 轴交于点 ,连接 , . 为线段 上的一个动点,过点 作 轴,交抛物线于点 ,交 于点 .
(1)求抛物线的表达式;
(2)过点 作 ,垂足为点 .设 点的坐标为 ,请用含 的代数式表示线段 的长,并求出当 为何值时 有最大值,最大值是多少?
(3)试探究点 在运动过程中,是否存在这样的点 ,使得以 , , 为顶点的三角形是等腰三角形.若存在,请求出此时点 的坐标;若不存在,请说明理由.

如图,抛物线 与 轴交于 , 两点,且 ,与 轴交于点 ,连接 ,抛物线对称轴为直线 , 为第一象限内抛物线上一动点,过点 作 于点 ,与 交于点 ,设点 的横坐标为 .
(1)求抛物线的表达式;
(2)当线段 的长度最大时,求 点的坐标;
(3)抛物线上是否存在点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求出 的值;若不存在,请说明理由.

如图,抛物线 与 轴交于点 和点 ,与 轴交于点 ,顶点为 ,连接 , , 与抛物线的对称轴 交于点 .
(1)求抛物线的表达式;
(2)点 是第一象限内抛物线上的动点,连接 , ,当 时,求点 的坐标;
(3)点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求点 的坐标;若不存在,请说明理由.

如图,抛物线 与 轴相交于 , 两点,与 轴相交于点 , , ,直线 是抛物线的对称轴,在直线 右侧的抛物线上有一动点 ,连接 , , , .
(1)求抛物线的函数表达式;
(2)若点 在 轴的下方,当 的面积是 时,求 的面积;
(3)在(2)的条件下,点 是 轴上一点,点 是抛物线上一动点,是否存在点 ,使得以点 , , , 为顶点,以 为一边的四边形是平行四边形,若存在,求出点 的坐标;若不存在,请说明理由.

如图,抛物线的顶点为 ,与 轴交于点 ,点 为其对称轴上的一个定点.
(1)求这条抛物线的函数解析式;
(2)已知直线 是过点 且垂直于 轴的定直线,若抛物线上的任意一点 到直线 的距离为 ,求证: ;
(3)已知坐标平面内的点 ,请在抛物线上找一点 ,使 的周长最小,并求此时 周长的最小值及点 的坐标.

如图,已知在平面直角坐标系 中,抛物线 的顶点为 ,与 轴的交点为 .过点 的直线 与抛物线交于另一点 (点 在对称轴左侧),点 在 的延长线上,连结 , , 和 .
(1)如图1,当 轴时,
①已知点 的坐标是 ,求抛物线的解析式;
②若四边形 是平行四边形,求证: .
(2)如图2,若 , ,是否存在这样的点 ,使四边形 是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.

已知直线 交 轴于点 ,交 轴于点 ,二次函数的图象过 , 两点,交 轴于另一点 , ,且对于该二次函数图象上的任意两点 , , , ,当 时,总有 .
(1)求二次函数的表达式;
(2)若直线 ,求证:当 时, ;
(3) 为线段 上不与端点重合的点,直线 过点 且交直线 于点 ,求 与 面积之和的最小值.
试题篮
()