已知二次函数的图象经过
,
两点.
(1)求,
的值.
(2)二次函数的图象与
轴是否有公共点?若有,求公共点的坐标;若没有,请说明情况.
已知二次函数图象的顶点坐标为
,该二次函数图象的对称轴与
轴的交点为
,
是这个二次函数图象上的点,
是原点.
(1)不等式是否成立?请说明理由;
(2)设是
的面积,求满足
的所有点
的坐标.
综合与探究
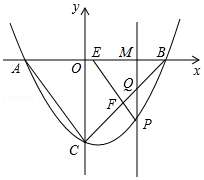
如图,抛物线与
轴交于
,
两点(点
在点
的左侧),与
轴交于点
,连接
,
.点
是第四象限内抛物线上的一个动点,点
的横坐标为
,过点
作
轴,垂足为点
,
交
于点
,过点
作
交
轴于点
,交
于点
.
(1)求,
,
三点的坐标;
(2)试探究在点运动的过程中,是否存在这样的点
,使得以
,
,
为顶点的三角形是等腰三角形.若存在,请直接写出此时点
的坐标;若不存在,请说明理由;
(3)请用含的代数式表示线段
的长,并求出
为何值时
有最大值.
已知抛物线与
轴相交于
、
两点(点
在点
的左侧),并与
轴相交于点
.
(1)求、
、
三点的坐标,并求
的面积;
(2)将抛物线向左或向右平移,得到抛物线
,且
与
轴相交于
、
两点(点
在点
的左侧),并与
轴相交于点
,要使△
和
的面积相等,求所有满足条件的抛物线的函数表达式.
已知抛物线与
轴相交于
和
两点,并与
轴相交于点
.抛物线
与
关于坐标原点对称,点
、
在
上的对应点分别为
、
(1)求抛物线的函数表达式;
(2)在抛物线上是否存在点
,使得△
的面积等于△
的面积?若存在,求点
的坐标;若不存在,请说明理由.
在同一直角坐标系中,抛物线与抛物线
关于
轴对称,
与
轴交于
、
两点,其中点
在点
的左侧.
(1)求抛物线,
的函数表达式;
(2)求、
两点的坐标;
(3)在抛物线上是否存在一点
,在抛物线
上是否存在一点
,使得以
为边,且以
、
、
、
四点为顶点的四边形是平行四边形?若存在,求出
、
两点的坐标;若不存在,请说明理由.

在平面直角坐标系中,点 为坐标原点,抛物线 经过点 和
(1)试判断该抛物线与 轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点 ,且与 轴交于点 ,同时满足以 、 、 为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.

某班"数学兴趣小组"对函数 的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量 的取值范围是全体实数, 与 的几组对应值列表如下:
|
|
|
|
|
|
|
0 |
1 |
2 |
|
3 |
|
|
|
|
3 |
|
|
|
0 |
|
0 |
|
3 |
|
其中, .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与 轴有 个交点,所以对应的方程 有 个实数根;
②方程 有 个实数根;
③关于 的方程 有4个实数根时, 的取值范围是 .

在平面直角坐标系中,抛物线
与
轴交于点
、
(点
在点
的左侧),与
轴交于点
.
(1)求直线的表达式;
(2)垂直于轴的直线
与抛物线交于点
,
,
,
,与直线
交于点
,
,若
,结合函数的图象,求
的取值范围.
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=- ,x1•x2=
,x1•x2=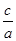 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=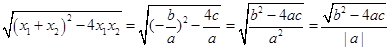 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.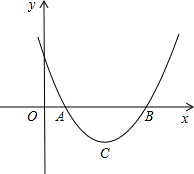
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
请阅读下列材料:若 是关于
是关于 的一元二次方程的两个根,则方程的两个根
的一元二次方程的两个根,则方程的两个根 和系数
和系数 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理.
. 我们把它们称为根与系数关系定理.
如果设二次函数 的图象与x轴的两个交点
的图象与x轴的两个交点 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
请你参考以上定理和结论,解答下列问题:
设二次函数 的图象与x轴的两个交点为
的图象与x轴的两个交点为 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然 为等腰三角形。
为等腰三角形。
(1)当 为等腰直角三角形时,求
为等腰直角三角形时,求 的值,
的值,
(2)当 为等边三角形时,求
为等边三角形时,求 的值,
的值,
(3)设抛物线 与
与 轴的两个交点为
轴的两个交点为 、
、 ,顶点为
,顶点为 ,且
,且 ,试问如何平移此抛物线,才能使
,试问如何平移此抛物线,才能使 ?
?
(年贵州省贵阳市)如图,经过点C(0,﹣4)的抛物线 (
( )与x轴相交于A(﹣2,0),B两点.
)与x轴相交于A(﹣2,0),B两点.

(1)a 0, 0(填“>”或“<”);
0(填“>”或“<”);
(2)若该抛物线关于直线x=2对称,求抛物线的函数表达式;
(3)在(2)的条件下,连接AC,E是抛物线上一动点,过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点E的坐标;若不存在,请说明理由.
(年青海省中考)如图,二次函数 的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(年新疆乌鲁木齐市)抛物线 与x轴交于A,B两点(OA<OB),与y轴交于点C.
与x轴交于A,B两点(OA<OB),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从点O出发,以每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间为t秒(0<t<2).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时, 的值最小,求出这个最小值并写出此时点E,P的坐标;
的值最小,求出这个最小值并写出此时点E,P的坐标;
②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
试题篮
()