初中数学二次函数的应用计算题

小明同学在一次社会实践活动中，通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律：

①该蔬菜的销售单价 $P$（单位：元 $/$千克）与时间 $x$（单位：月份）满足关系： $P=9-x$；

②该蔬菜的平均成本 $y$（单位：元 $/$千克）与时间 $x$（单位：月份）满足二次函数关系 $y=a{x}^2+\mathit{bx}+10$．

已知4月份的平均成本为2元 $/$千克，6月份的平均成本为1元 $/$千克．

（1）求该二次函数的解析式；

（2）请运用小明统计的结论，求出该蔬菜在第几月份的平均利润 $L$（单位：元 $/$千克）最大？最大平均利润是多少？（注：平均利润 $=$销售单价 $-$平均成本）

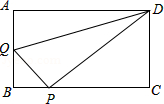
已知：如图所示，在平面直角坐标系 $\mathit{xOy}$中，四边形 $\mathit{OABC}$是矩形， $\mathit{OA}=4$， $\mathit{OC}=3$，动点 $P$从点 $C$出发，沿射线 $\mathit{CB}$方向以每秒2个单位长度的速度运动；同时，动点 $Q$从点 $O$出发，沿 $x$轴正半轴方向以每秒1个单位长度的速度运动．设点 $P$、点 $Q$的运动时间为 $t\left(s\right)$．

（1）当 $t=1s$时，求经过点 $O$， $P$， $A$三点的抛物线的解析式；

（2）当 $t=2s$时，求 $\tan \angle \mathit{QPA}$的值；

（3）当线段 $\mathit{PQ}$与线段 $\mathit{AB}$相交于点 $M$，且 $\mathit{BM}=2\mathit{AM}$时，求 $t\left(s\right)$的值；

（4）连接 $\mathit{CQ}$，当点 $P$， $Q$在运动过程中，记 $\mathit{\Delta CQP}$与矩形 $\mathit{OABC}$重叠部分的面积为 $S$，求 $S$与 $t$的函数关系式．

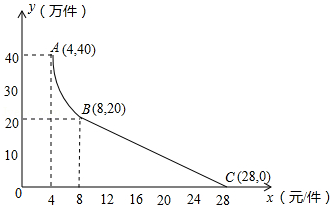
某电子科技有限公司用160万元，作为新产品的研发费用，成功研制出了一种市场急需的电子产品，已于当年投入生产并进行销售．已知生产这种电子产品的成本为4元 $/$件，在销售过程中发现：每年的年销售量 $y$（万件）与销售价格 $x$（元 $/$件）的关系如图所示，其中 $\mathit{AB}$为反比例函数图象的一部分， $\mathit{BC}$为一次函数图象的一部分．设公司销售这种电子产品的年利润为 $s$（万元）．（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本． $)$

（1）请求出 $y$（万件）与 $x$（元 $/$件）之间的函数关系式；

（2）求出第一年这种电子产品的年利润 $s$（万元）与 $x$（元 $/$件）之间的函数关系式，并求出第一年年利润的最大值．

（3）假设公司的这种电子产品第一年恰好按年利润 $s$（万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格 $x$（元 $)$定在8元以上 $(x>8)$，当第二年的年利润不低于103万元时，请结合年利润 $s$（万元）与销售价格 $x$（元 $/$件）的函数示意图，求销售价格 $x$（元 $/$件）的取值范围．

如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点 $A$．甲从中山路上点 $B$出发，骑车向北匀速直行；与此同时，乙从点 $A$出发，沿北京路步行向东匀速直行．设出发 $\mathit{xmin}$时，甲、乙两人与点 $A$的距离分别为 $y_{1}m$、 $y_{2}m$．已知 $y_1$、 $y_2$与 $x$之间的函数关系如图②所示．

（1）求甲、乙两人的速度；

（2）当 $x$取何值时，甲、乙两人之间的距离最短？

超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加 $x$元，每天售出 $y$件．

（1）请写出 $y$与 $x$之间的函数表达式；

（2）当 $x$为多少时，超市每天销售这种玩具可获利润2250元？

（3）设超市每天销售这种玩具可获利 $w$元，当 $x$为多少时 $w$最大，最大值是多少？

已知矩形 $\mathit{ABCD}$中， $\mathit{AB}=5\mathit{cm}$，点 $P$为对角线 $\mathit{AC}$上的一点，且 $\mathit{AP}=2\sqrt{5}\mathit{cm}$．如图①，动点 $M$从点 $A$出发，在矩形边上沿着 $A\to B\to C$的方向匀速运动（不包含点 $C$）.设动点 $M$的运动时间为 $t\left(s\right)$， $\mathit{\Delta APM}$的面积为 $S\left(c{m}^2\right)$， $S$与 $t$的函数关系如图②所示．

（1）直接写出动点 $M$的运动速度为　    　 $\mathit{cm}/s$， $\mathit{BC}$的长度为　 　 $\mathit{cm}$；

（2）如图③，动点 $M$重新从点 $A$出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点 $N$从点 $D$出发，在矩形边上沿着 $D\to C\to B$的方向匀速运动，设动点 $N$的运动速度为 $v(\mathit{cm}/s)$．已知两动点 $M$， $N$经过时间 $x\left(s\right)$在线段 $\mathit{BC}$上相遇（不包含点 $C$），动点 $M$， $N$相遇后立即同时停止运动，记此时 $\mathit{\Delta APM}$与 $\mathit{\Delta DPN}$的面积分别为 $S_1\left(c{m}^2\right)$， $S_2\left(c{m}^2\right)$

①求动点 $N$运动速度 $v(\mathit{cm}/s)$的取值范围；

②试探究 $S_1·S_2$是否存在最大值，若存在，求出 $S_1·S_2$的最大值并确定运动时间 $x$的值；若不存在，请说明理由．

草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量 $y$ （千克）与销售单价 $x$ （元）符合一次函数关系，如图是 $y$ 与 $x$ 的函数关系图象．

（1）求 $y$ 与 $x$ 的函数解析式（也称关系式）；

（2）设该水果销售店试销草莓获得的利润为 $W$ 元，求 $W$ 的最大值．

如图，在矩形 $\mathit{OABC}$中， $\mathit{OA}=3$， $\mathit{OC}=2$， $F$是 $\mathit{AB}$上的一个动点 $(F$不与 $A$， $B$重合），过点 $F$的反比例函数 $y=\frac{k}{x}(k>0)$的图象与 $\mathit{BC}$边交于点 $E$．

（1）当 $F$为 $\mathit{AB}$的中点时，求该函数的解析式；

（2）当 $k$为何值时， $\mathit{\Delta EFA}$的面积最大，最大面积是多少？

旅游公司在景区内配置了50辆观光车供游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金 $x$（元）是5的倍数．发现每天的营运规律如下：当 $x$不超过100元时，观光车能全部租出；当 $x$超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．

（1）优惠活动期间，为使观光车全部租出且每天的净收入为正，则每辆车的日租金至少应为多少元？（注：净收入 $=$租车收入 $-$管理费）

（2）当每辆车的日租金为多少元时，每天的净收入最多？

已知：如图，在矩形 $\mathit{ABCD}$中， $\mathit{AB}=6\mathit{cm}$， $\mathit{BC}=8\mathit{cm}$，对角线 $\mathit{AC}$， $\mathit{BD}$交于点 $O$．点 $P$从点 $A$出发，沿 $\mathit{AD}$方向匀速运动，速度为 $1\mathit{cm}/s$；同时，点 $Q$从点 $D$出发，沿 $\mathit{DC}$方向匀速运动，速度为 $1\mathit{cm}/s$；当一个点停止运动时，另一个点也停止运动．连接 $\mathit{PO}$并延长，交 $\mathit{BC}$于点 $E$，过点 $Q$作 $\mathit{QF}//\mathit{AC}$，交 $\mathit{BD}$于点 $F$．设运动时间为 $t\left(s\right)(0<t<6)$，解答下列问题：

（1）当 $t$为何值时， $\mathit{\Delta AOP}$是等腰三角形？

（2）设五边形 $\mathit{OECQF}$的面积为 $S\left(c{m}^2\right)$，试确定 $S$与 $t$的函数关系式；

（3）在运动过程中，是否存在某一时刻 $t$，使 $S_{\mathit{五边形}\mathit{OECQF}}:S_{\mathit{\Delta ACD}}=9:16$？若存在，求出 $t$的值；若不存在，请说明理由；

（4）在运动过程中，是否存在某一时刻 $t$，使 $\mathit{OD}$平分 $\angle \mathit{COP}$？若存在，求出 $t$的值；若不存在，请说明理由．

如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用 $y=a{x}^2+\mathit{bx}(a\ne 0)$表示．已知抛物线上 $B$， $C$两点到地面的距离均为 $\frac{3}{4}m$，到墙边 $\mathit{OA}$的距离分别为 $\frac{1}{2}m$， $\frac{3}{2}m$．

（1）求该拋物线的函数关系式，并求图案最高点到地面的距离；

（2）若该墙的长度为 $10m$，则最多可以连续绘制几个这样的拋物线型图案？

在边长为2的等边三角形 $\mathit{ABC}$ 中， $P$ 是 $\mathit{BC}$ 边上任意一点，过点 $P$ 分别作 $\mathit{PM}\perp \mathit{AB}$ ， $\mathit{PN}\perp \mathit{AC}$ ， $M$ 、 $N$ 分别为垂足．

（1）求证：不论点 $P$ 在 $\mathit{BC}$ 边的何处时都有 $\mathit{PM}+\mathit{PN}$ 的长恰好等于三角形 $\mathit{ABC}$ 一边上的高；

（2）当 $\mathit{BP}$ 的长为何值时，四边形 $\mathit{AMPN}$ 的面积最大，并求出最大值．

在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=3$ ， $\mathit{AD}=4$ ，动点 $Q$ 从点 $A$ 出发，以每秒1个单位的速度，沿 $\mathit{AB}$ 向点 $B$ 移动；同时点 $P$ 从点 $B$ 出发，仍以每秒1个单位的速度，沿 $\mathit{BC}$ 向点 $C$ 移动，连接 $\mathit{QP}$ ， $\mathit{QD}$ ， $\mathit{PD}$ ．若两个点同时运动的时间为 $x$ 秒 $(0<x⩽3)$ ，解答下列问题：

（1）设 $\mathit{\Delta QPD}$ 的面积为 $S$ ，用含 $x$ 的函数关系式表示 $S$ ；当 $x$ 为何值时， $S$ 有最大值？并求出最小值；

（2）是否存在 $x$ 的值，使得 $\mathit{QP}\perp \mathit{DP}$ ？试说明理由．

空地上有一段长为 $a$ 米的旧墙 $\mathit{MN}$ ，某人利用旧墙和木栏围成一个矩形菜园 $\mathit{ABCD}$ ，已知木栏总长为100米．

（1）已知 $a=20$ ，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．如图1，求所利用旧墙 $\mathit{AD}$ 的长；

（2）已知 $0<a<50$ ，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园 $\mathit{ABCD}$ 的面积最大，并求面积的最大值．

如图，在足够大的空地上有一段长为 $a$ 米的旧墙 $\mathit{MN}$ ，某人利用旧墙和木栏围成一个矩形菜园 $\mathit{ABCD}$ ，其中 $\mathit{AD}⩽\mathit{MN}$ ，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

（1）若 $a=20$ ，所围成的矩形菜园的面积为450平方米，求所利用旧墙 $\mathit{AD}$ 的长；

（2）求矩形菜园 $\mathit{ABCD}$ 面积的最大值．