农经公司以30元 千克的价格收购一批农产品进行销售,为了得到日销售量 (千克)与销售价格 (元 千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格 (元 千克) |
30 |
35 |
40 |
45 |
50 |
日销售量 (千克) |
600 |
450 |
300 |
150 |
0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定 与 之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出 元 的相关费用,当 时,农经公司的日获利的最大值为2430元,求 的值.(日获利 日销售利润 日支出费用)
如图①,菱形 中, ,动点 从点 出发,沿折线 运动到点 停止,动点 从点 出发,沿线段 运动到点 停止,它们运动的速度相同,设点 出发 时, 的面积为 .已知 与 之间的函数关系如图②所示,其中 、 为线段,曲线 为抛物线的一部分.请根据图中的信息,解答下列问题:
(1)当 时, 的面积 (填“变”或“不变” ;
(2)分别求出线段 ,曲线 所对应的函数表达式;
(3)当 为何值时, 的面积是 ?

某品牌牛奶专营店销售一款牛奶,售价是在进价的基础上加价 出售,每月的销售额可以达到9.6万元,但每月需支出2.45万元的固定费用及进价的 的其他费用.
(1)如果该款牛奶每月所获的利润要达到1万元,那么 的值是多少?(利润 售价 进价 固定费用 其他费用)
(2)现这款牛奶的售价为64元 盒,根据市场调查,这款牛奶如果售价每降低 ,销售量将上升 ,求这款牛奶调价销售后,每月可获的最大利润.
某品牌牛奶专营店销售一款牛奶,售价是在进价的基础上加价 出售,每月的销售额可以达到9.6万元,但每月需支出2.45万元的固定费用及进价的 的其他费用.
(1)如果该款牛奶每月所获的利润要达到1万元,那么 的值是多少?(利润 售价 进价 固定费用 其他费用)
(2)现这款牛奶的售价为64元 盒,根据市场调查,这款牛奶如果售价每降低 ,销售量将上升 ,求这款牛奶调价销售后,每月可获的最大利润.
怡然美食店的 、 两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低 种菜品的售价,同时提高 种菜品的售价,售卖时发现, 种菜品售价每降0.5元可多卖1份; 种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
某宾馆拥有客房100间,经营中发现:每天入住的客房数 (间)与其价格 (元) 满足一次函数关系,部分对应值如表:
(元) |
180 |
260 |
280 |
300 |
(间) |
100 |
60 |
50 |
40 |
(1)求 与 之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润 当日房费收入 当日支出)
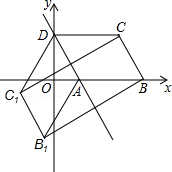
如图,已知 的三个顶点 、 、 , ,作 关于直线 的对称图形
(1)若 ,试求四边形 面积 的最大值;
(2)若点 恰好落在 轴上,试求 的值.
某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过 人时,每增加1人,人均收费降低1元;超过 人时,人均收费都按照 人时的标准.设景点接待有 名游客的某团队,收取总费用为 元.
(1)求 关于 的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求 的取值范围.
图中是抛物线拱桥, 处有一照明灯,水面 宽 ,从 、 两处观测 处,仰角分别为 、 ,且 , ,以 为原点, 所在直线为 轴建立直角坐标系.
(1)求点 的坐标;
(2)水面上升 ,水面宽多少 取1.41,结果精确到 ?

试题篮
()