如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

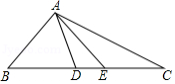
如图,在 中, ,点 , 分别在边 , 上, ,连结 , .
(1)若 ,求 , 的度数;
(2)写出 与 之间的关系,并说明理由.

如图,在 中, ,以 为直径的半圆 交 于点 ,过点 作半圆 的切线,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

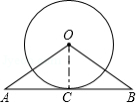
如图,在 中, ,以点 为圆心, 为半径的圆交 于点 ,点 在边 上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)已知 , ,求 的半径.

《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,在地面上沿着杆的影子的方向取一点 ,使 , 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 , 两点间的距离为10步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点 , , 的位置如图所示.使用直尺和圆规,在图中作 的中点 (保留作图痕迹);

(2)在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线 表示的方向为南北方向,完成如下证明.
证明:在 中, , 是 的中点,
(填推理的依据).
直线 表示的方向为东西方向,
直线 表示的方向为南北方向.
如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .

问题:如图,在 中, .在 的延长线上取点 , ,作 ,使 .若 , ,求 的度数.
答案: .
思考:(1)如果把以上“问题”中的条件“ ”去掉,其余条件不变,那么 的度数会改变吗?说明理由.
(2)如果把以上“问题”中的条件“ ”去掉,再将“ ”改为“ ”,其余条件不变,求 的度数.
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
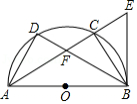
如图, 是半圆 的直径, , 是半圆 上不同于 , 的两点, , 与 相交于点 . 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)求证: ;
(2)若 ,求证: 平分 .
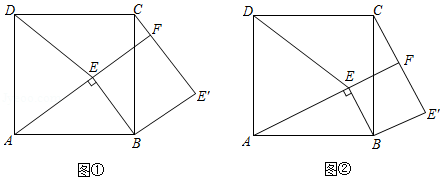
综合与实践
问题情境:
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 .延长 交 于点 ,连接 .
猜想证明:
(1)试判断四边形 的形状,并说明理由;
(2)如图②,若 ,请猜想线段 与 的数量关系并加以证明;
解决问题:
(3)如图①,若 , ,请直接写出 的长.
试题篮
()