如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )

A.150°B.130°C.120°D.100°
如图,在 中, , ,垂足为 , 平分 ,交 于点 ,交 于点 .若 , ,则 的长为
A. B. C. D.
如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.

已知在菱形 中, ,对角线 、 相交于点 ,点 是线段 上一动点(不与点 , 重合),连接 ,以 为边在 的右侧作菱形 ,且 .
(1)如图1,若点 落在线段 上,请判断:线段 与线段 的数量关系是
(2)如图2,若点 不在线段 上,其它条件不变,(1)中的结论是否仍然成立?请给出判断并予以证明;
(3)若点
,
,
三点在同一直线上,其它条件不变,请直接写出线段
与线段
的数量关系.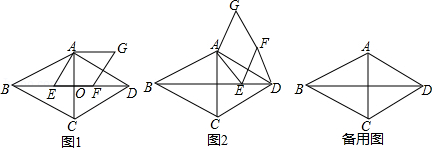
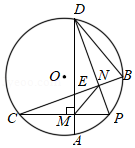
如图, 是 的直径,点 ,点 在 上, , 与 相交于点 , 与 相切于点 ,与 延长线相交于点 .
(1)求证: .
(2)若 , ,求 的半径.

在菱形 中, ,点 是射线 上一动点,以 为边向右侧作等边 ,点 的位置随着点 的位置变化而变化.

(1)如图1,当点 在菱形 内部或边上时,连接 , 与 的数量关系是 , 与 的位置关系是 ;
(2)当点 在菱形 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图4,当点 在线段 的延长线上时,连接 ,若 , ,求四边形 的面积.
如图,在 中,点 为 的中点,弦 、 互相垂直,垂足为 , 分别与 、 相交于点 、 ,连接 、 .
(1)求证: 为 的中点.
(2)若 的半径为8, 的度数为 ,求线段 的长.
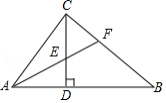
如图,在 中, 和 是高, ,点 是 的中点, 与 、 分别交于点 、 , .有下列结论:① ;② ;③ ;④ .其中正确的有

A.1个B.2 个C.3 个D.4个
中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
已知抛物线经过点
和点
,与
轴交于另一点
,顶点为
.
(1)求抛物线的解析式,并写出顶点的坐标;
(2)如图,点,
分别在线段
,
上(点
不与点
,
重合),且
,
,直接写出线段
的长.

如图,在 中, 为斜边 的中线,过点 作 于点 ,延长 至点 ,使 ,连接 , ,点 在线段 上,连接 ,且 , , .下列结论:
① ;
②四边形 是平行四边形;
③ ;
④ .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在 中, ,以斜边 上的中线 为直径作 ,与 交于点 ,与 的另一个交点为 ,过 作 ,垂足为 .
(1)求证: 是 的切线;
(2)若 的直径为5, ,求 的长.

试题篮
()