初中数学含30度角的直角三角形试题

如图，矩形 $\mathit{ABCD}$， $\angle \mathit{BAC}=60°$，以点 $A$为圆心，以任意长为半径作弧分别交 $\mathit{AB}$， $\mathit{AC}$于点 $M$， $N$两点，再分别以点 $M$， $N$为圆心，以大于 $\frac{1}{2}\mathit{MN}$的长作半径作弧交于点 $P$，作射线 $\mathit{AP}$交 $\mathit{BC}$于点 $E$，若 $\mathit{BE}=1$，则矩形 $\mathit{ABCD}$的面积等于　　．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle A=30°$， $\mathit{BC}=1$，点 $D$， $E$分别是直角边 $\mathit{BC}$， $\mathit{AC}$的中点，则 $\mathit{DE}$的长为 $($　　 $)$

A．1B．2C． $\sqrt{3}$D． $1+\sqrt{3}$

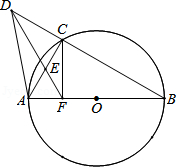
已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形

（1）求证：△DFB是等腰三角形；

（2）若 $\mathit{DA}＝\sqrt{7}\mathit{AF}$，求证： $\mathit{CF}\perp \mathit{AB}$．

如图，在四边形ABCD中，对角线AC、BD相交于点E， $\angle \mathit{DAB}＝\angle \mathit{CDB}＝90°$， $\angle \mathit{ABD}＝45°$， $\angle \mathit{DCA}＝30°$， $\mathit{AB}＝\sqrt{6}$，则AE＝　　（提示：可过点A作BD的垂线）

已知Rt△ OAB，∠ OAB＝90°，∠ ABO＝30°，斜边 OB＝4，将Rt△ OAB绕点 O顺时针旋转60°，如图1，连接 BC．

（1）填空：∠ OBC＝ 　　°；

（2）如图1，连接 AC，作 OP⊥ AC，垂足为 P，求 OP的长度；

（3）如图2，点 M， N同时从点 O出发，在△ OCB边上运动， M沿 O→ C→ B路径匀速运动， N沿 O→ B→ C路径匀速运动，当两点相遇时运动停止，已知点 M的运动速度为1.5单位/秒，点 N的运动速度为1单位/秒，设运动时间为 x秒，△ OMN的面积为 y，求当 x为何值时 y取得最大值？最大值为多少？

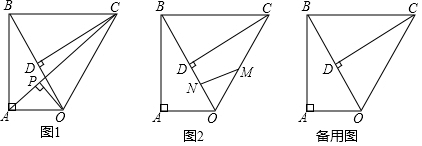
如图，在四边形 ABCD中， BD平分∠ ABC，∠ BAD＝∠ BDC＝90°， E为 BC的中点， AE与 BD相交于点 F．若 BC＝4，∠ CBD＝30°，则 DF的长为（　　）

A．

$\frac{2}{5}\sqrt{3}$

B．

$\frac{2}{3}\sqrt{3}$

C．

$\frac{3}{4}\sqrt{3}$

D．

$\frac{4}{5}\sqrt{3}$

如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点，当△APB为直角三角形时，AP＝　    　．

如图，在Rt△ ABC中，∠ C＝90°，∠ B＝30°，以 A为圆心适当长为半径画弧，分别交 AB、 AC于点 M、 N，分别以点 M、 N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧交于点 P，作射线 AP交 BC于点 D，再作射线 DE交 AB于点 E，则下列结论错误的是（　　）

A．	∠ADB＝120°	B．	S △ ADC：S △ ABC＝1：3
C．	若CD＝2，则BD＝4	D．	DE垂直平分AB

把一副三角板按如图放置，其中∠ABC＝∠DEB＝90°，∠A＝45°，∠D＝30°，斜边AC＝BD＝10，若将三角板DEB绕点B逆时针旋转45°得到△D′E′B，则点A在△D′E′B的（　　）

A．内部B．外部

C．边上D．以上都有可能

如图，△ABC中，∠C＝90°，∠A＝30°，AB＝12，则BC＝（　　）

A．6B． $6\sqrt{2}$C． $6\sqrt{3}$D．12

如图，在 中， ， ， ．

（1）利用尺规作线段 的垂直平分线 ，垂足为 ，交 于点 ，（保留作图痕迹，不写作法）

（2）若 的周长为 ，先化简 ，再求 的值．

如图，Rt△ ABC中，∠ B＝30°，∠ ACB＝90°， CD⊥ AB交 AB于 D，以 CD为较短的直角边向△ CDB的同侧作Rt△ DEC，满足∠ E＝30°，∠ DCE＝90°，再用同样的方法作Rt△ FGC，∠ FCG＝90°，继续用同样的方法作Rt△ HIC，∠ HCI＝90°．若 AC＝ a，求 CI的长．

如图，在四边形 $\mathit{ABCD}$中， $\mathit{AB}=\mathit{CB}$， $\mathit{AD}=\mathit{CD}$，我们把这种两组邻边分别相等的四边形叫做“筝形”．筝形 $\mathit{ABCD}$的对角线 $\mathit{AC}$， $\mathit{BD}$相交于点 $O$．以点 $B$为圆心， $\mathit{BO}$长为半径画弧，分别交 $\mathit{AB}$， $\mathit{BC}$于点 $E$， $F$．若 $\angle \mathit{ABD}=\angle \mathit{ACD}=30°$， $\mathit{AD}=1$，则 $\stackrel{̂}{\mathit{EF}}$的长为　   　（结果保留 $\pi )$．

数学家笛卡尔在《几何》一书中阐述了坐标几何的思想，主张取代数和几何中最好的东西，互相以长补短．在菱形中，，．如图，建立平面直角坐标系，使得边在轴正半轴上，点在轴正半轴上，则点的坐标是　 　．

如图，在平面直角坐标系中， $\text{Rt}\Delta \text{OAB}$ 的斜边 $\mathit{OA}$ 在第一象限，并与 $x$ 轴的正半轴夹角为 $30°$ ． $C$ 为 $\mathit{OA}$ 的中点， $\mathit{BC}=1$ ，则点 $A$ 的坐标为 $($ 　　 $)$

A．

$(\sqrt{3}$ ， $\sqrt{3})$

B．

$(\sqrt{3}$ ， $1)$

C．

$(2,1)$

D．

$(2,\sqrt{3})$