在图1,2,3中,已知,
,点
为线段
上的动点,连接
,以
为边向上作菱形
,且
.
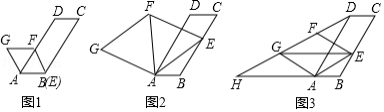
(1)如图1,当点与点
重合时,
;
(2)如图2,连接.
①填空:
(填“
”,“
“,“
”
;
②求证:点在
的平分线上;
(3)如图3,连接,
,并延长
交
的延长线于点
,当四边形
是平行四边形时,求
的值.
如图,的对角线
、
相交于点
,
经过
,分别交
、
于点
、
,
的延长线交
的延长线于
.
(1)求证:;
(2)若,
,
,求
的长.

在平面直角坐标系中,直线 交 轴于点 ,交 轴于点 .

(1) 的值是 ;
(2)点 是直线 上的一个动点,点 和点 分别在 轴和 轴上.
①如图,点 为线段 的中点,且四边形 是平行四边形时,求 的周长;
②当 平行于 轴, 平行于 轴时,连接 ,若 的面积为 ,请直接写出点 的坐标.
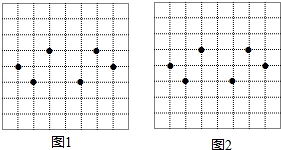
图1,图2都是的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点
(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);
(2)图1中所画的平行四边形的面积为 .
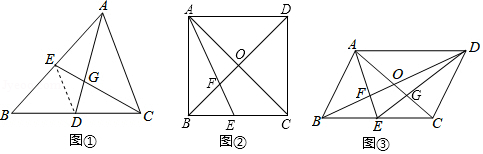
教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
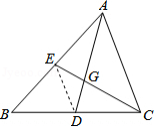
例2 如图,在中,
,
分别是边
,
的中点,
,
相交于点
,求证:
证明:连结.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在中,对角线
、
交于点
,
为边
的中点,
、
交于点
.
(1)如图②,若为正方形,且
,则
的长为 .
(2)如图③,连结交
于点
,若四边形
的面积为
,则
的面积为 .
如图,在平行四边形中,点
是对角线
的中点,点
是
上一点,且
,连接
并延长交
于点
.过点
作
的垂线,垂足为
,交
于点
.
(1)若,
,求
的面积;
(2)若,求证:
.

在中,
平分
交
于点
.

(1)如图1,若,
,求
的面积;
(2)如图2,过点作
,交
的延长线于点
,分别交
,
于点
,
,且
.求证:
.
如图,在 中, 是对角线 、 的交点, , ,垂足分别为点 、 .
(1)求证: .
(2)若 , ,求 的值.
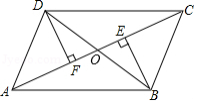
如图,已知 , , ,垂足为 .
(1)求证: ;
(2)只需添加一个条件,即 ,可使四边形 为矩形.请加以证明.

试题篮
()