已知 是 的任意一条直径.
(1)用图1,求证: 是以直径 所在直线为对称轴的轴对称图形;
(2)已知 的面积为 ,直线 与 相切于点 ,过点 作 ,垂足为 ,如图2.
求证:① ;
②改变图2中切点 的位置,使得线段 时, .

小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


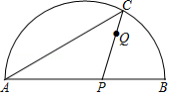
如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .
(1)求 的长.
(2)点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.

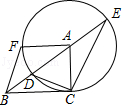
如图,在Rt△ ACB中,∠ ACB=90°,以点 A为圆心, AC长为半径的圆交 AB于点 D, BA的延长线交⊙ A于点 E,连接 CE, CD, F是⊙ A上一点,点 F与点 C位于 BE两侧,且∠ FAB=∠ ABC,连接 BF.
(1)求证:∠ BCD=∠ BEC;
(2)若 BC=2, BD=1,求 CE的长及sin∠ ABF的值.
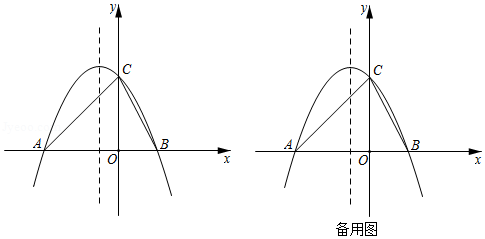
在平面直角坐标系中,抛物线 过点 , ,与 轴交于点 ,顶点为点 .
(1)求抛物线的解析式;
(2)点 为直线 上的一个动点,连接 ;
①如图1,是否存在点 ,使 ?若存在,求出所有满足条件的点 的坐标;若不存在,请说明理由;
②如图2,点 在 轴上方,连接 交抛物线于点 , ,点 在第三象限抛物线上,连接 ,当 时,请直接写出点 的坐标.

如图,在 中, ,点 为 边上一点,以点 为圆心, 长为半径的圆与边 相交于点 ,连接 ,当 为 的切线时.
(1)求证: ;
(2)若 , 的半径为1,请直接写出 的长为 .

如图,抛物线 与 轴交于点 ,点 ,与 轴交于点 ,抛物线的对称轴为直线 ,点 坐标为 .
(1)求抛物线表达式;
(2)在抛物线上是否存在点 ,使 ,如果存在,求出点 坐标;如果不存在,请说明理由;
(3)在(2)的条件下,若点 在 轴上方,点 是直线 上方抛物线上的一个动点,求点 到直线 的最大距离;
(4)点 是线段 上的动点,点 是线段 上的动点,点 是线段 上的动点,三个动点都不与点 , , 重合,连接 , , ,得到 ,直接写出 周长的最小值.
(1)如图①,点 在 上,点 在 上, , .求证: .
(2)如图②, 为 上一点,按以下步骤作图:
①连接 ;
②以点 为圆心, 长为半径作弧,交 于点 ;
③在射线 上截取 ;
④连接 .
若 ,求 的半径.

如图,是
的直径,
、
两点在
的延长线上,
是
上的点,且
,延长
至
,使得
,设
,
.
(1)求证:;
(2)求,
的长;
(3)若点在
、
、
三点确定的圆上,求
的长.

请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .
如图,是
与弦
所围成的图形的内部的一定点,
是弦
上一动点,连接
并延长交
于点
,连接
.已知
,设
,
两点间的距离为
,
,
两点间的距离为
,
,
两点间的距离为
.
小腾根据学习函数的经验,分别对函数,
随自变量
的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量的值进行取点、画图、测量,分别得到了
,
与
的几组对应值;
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
(2)在同一平面直角坐标系中,描出补全后的表中各组数值所对应的点
,
,并画出函数
,
的图象;

(3)结合函数图象,解决问题:当为等腰三角形时,
的长度约为
.
试题篮
()