通过对下面数学模型的研究学习,解决问题.
【模型呈现】
如图,在 , ,将斜边 绕点 顺时针旋转 得到 ,过点 作 于点 ,可以推理得到 ,进而得到 , .
我们把这个数学模型称为“ 型”.
推理过程如下:

【模型应用】
如图,在 内接于 , , ,将斜边 绕点 顺时针旋转一定的角度得到 ,过点 作 于点 , , ,连接 交 于点 .

(1)求证: 是 的切线;
(2)连接 交 于点 ,连接 .求证: .
如图, 为 直径, 为 上一点,点 是 的中点, 于 , 于 .
(1)判断 与 的位置关系,并证明你的结论;
(2)若 ,求 的长度.

已知:△ ABC内接于⊙ O, D是 上一点, ,垂足为 H.
(1)如图1,当圆心 O在 AB边上时,求证: ;
(2)如图2,当圆心 O在△ ABC外部时,连接 AD、 CD, AD与 BC交于点 P,求证: ;
(3)在(2)的条件下,如图3,连接 BD, E为⊙ O上一点,连接 DE交 BC于点 Q、交 AB于点 N,连接 OE, BF为⊙ O的弦, 于点 R交 DE于点 G,若 , , , ,求 BF的长.

如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.

如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知 .
(1)求证:①直线AB是⊙O的切线;② ;
(2)求CD的长.

如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且 ,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6, ,求弦BD的长.

如图,在⊙ O中, B是⊙ O上的一点,∠ ABC=120°,弦 AC=2 ,弦 BM平分∠ ABC交 AC于点 D,连接 MA, MC.
(1)求⊙ O半径的长;
(2)求证: AB+ BC= BM.

如图,在△ ABC中,∠ ABC=90°,以 AB的中点 O为圆心, OA为半径的圆交 AC于点 D, E是 BC的中点,连结 DE、 OE.
(1)判断 DE与⊙ O的位置关系,并说明理由.
(2)求证: BC 2=2 CD• OE.
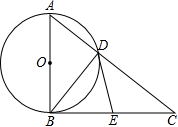
如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.
(1)求证:DF是⊙O的切线;
(2)求证:OC2=OE•OP;
(3)求线段EG的长.

如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
(1)求⊙O的半径;
(2)点E为圆上一点,∠ECD=15°,将 沿弦CE翻折,交CD于点F,求图中阴影部分的面积.

如图,已知⊙ O的直径为 AB, AC⊥ AB于点 A, BC与⊙ O相交于点 D,在 AC上取一点 E,使得 ED= EA.
(1)求证: ED是⊙ O的切线;
(2)当 OE=10时,求 BC的长.

如图,在平面直角坐标系中, O(0,0), A(0,﹣6), B(8,0)三点在⊙ P上, M为劣弧的 中点.
(1)求圆的半径及圆心 P的坐标;
(2)求证: AM是∠ OAB的平分线;
(3)连接 BM并延长交 y轴于点 N,求 N, M点的坐标.

我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点 在以
在以 (南北方向)为直径的
(南北方向)为直径的 上,
上, ,
, 交
交 于点
于点 ,垂足为
,垂足为 ,
, ,弦
,弦 、
、 分别交
分别交 于点
于点 、
、 ,且
,且 .
.
(1)比较 与 的大小;
(2)若 ,求证:
,求证: ;
;
(3)设直线 、
、 相交所成的锐角为
相交所成的锐角为 ,试确定
,试确定 时,点
时,点 的位置.
的位置.

如图,线段 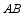 是
是 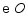 的直径,弦
的直径,弦 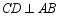 于点
于点 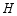 ,点
,点 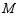 是
是 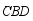 上任意一点,
上任意一点, 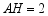 ,
, 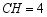 .
.
(1)求 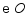 的半径
的半径 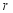 的长度;
的长度;
(2)求 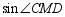 ;
;
(3)直线 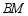 交直线
交直线 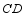 于点
于点 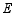 ,直线
,直线 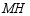 交
交 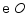 于点
于点 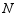 ,连接
,连接 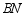 交
交 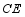 于点
于点 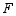 ,求
,求 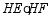 的值.
的值.
试题篮
()