将□ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处．求证：△ABE≌△AGF.
连结AC，若□ABCD的面积等于8，
，
，试求y与x之间的函数关系式．
如图，正方形
中,点F在边BC上，E在边BA的延长线上.若
按顺时针方向旋转后恰好与
重合.则旋转中心是点 ；
最少旋转了 度；在（1）的条件下，若
,求四边形
的面积. 
已知，正方形ABCD中，∠MAN="45°," ∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数
量关系： ；如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由．如果成立请证明；
如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．
（可利用（2）得到的结论） 
如图（1），凸四边形
，如果点
满足
，且
，则称点为四边形的一个半等角点．在图（2）正方形
内画一个半等角点，且满足
；在图（3）四边形
中画出一个半等角点，
保留画图痕迹（不需写出画法）．
如图25-1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF=
∠BAD.求证:EF＝BE＋FD;如图25-2在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF=
∠BAD, (1)中的结论是否仍然成立？不用证明. 如图25-3在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF=
∠BAD, (1)中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.
书籍是人类进步的阶梯！为爱护书一般都将书本用封皮包好．
现有精装词典长、宽、厚尺寸如图（1）所示（单位：cm），若按图（2）的包书方式，将封面和封底各折进去3cm．试用含a、b、c的代数式分别表示词典封皮（包书纸）的长是 cm，宽是___________cm；
在如图（4）的矩形包书纸皮示意图中，虚线为折痕，阴影是裁剪掉的部分，四角均为大小相同的正方形，正方形的边长即为折叠进去的宽度．
（1）若有一数学课本长为26cm、宽为18.5cm、厚为1cm，小海宝用一张面积为1260 cm2的矩形纸包好了这本数学书，封皮展开后如图（4）所示．若设正方形的边长（即折叠的宽度）为x cm，则包书纸长为 cm，宽为 cm（用含x的代数式表示）．
（2）请帮小海宝列好方程，求出第（1）题中小正方形的边长x cm．
两个全等的直角三角形ABC和DEF重叠在一起，其中∠A=60°，AC=1．固定△ABC不动，将△DEF进行如下操作： 如图1，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连结DC、CF、FB，四边形CDBF的形状在不断的变化，但它的面积不变化，四边形CDBF面积为 ▲ ；
如图2，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．
如图3，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连结AE，请你求出sin∠AED的值．
如图，在矩形中，
平分
，交
于点
,点
在边
上.
如果
，那么
和
相等吗？证明你的结论
.如果
，那么与有怎样的位置关系？证明你的结论.
（本题
满分6分）如图，在△ABC中，∠ACB＝90°，D是BC中点，DE⊥BC，CE∥AD，若AC＝2，CE＝4．求四边形ACEB的周长．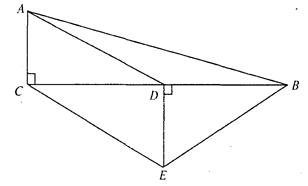
如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．求证：△BDF≌△CDE；
若AB＝AC，求证：四边形BFCE是菱形．
在长方形中画出5条线，把它分成的块数与画线的方式有直接关系.按如图1的方式画线，可以把它分成10块.请你在图2中画出5条线，使得把这个长方形分成的块数最少（重合的线只看做一条），最少可分成 块；
请你在图2中画出5条线，使得把这个长方形分成的块数最多，最多可分成 块.
(画出图形不写画法和理由)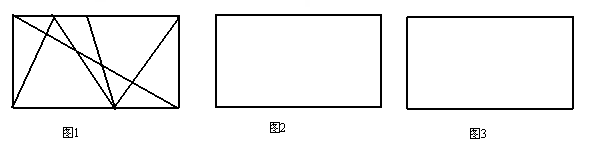
试题篮
()
粤公网安备 44130202000953号
是同一直线上的三个点，四边形
与四边形
都是正方形，连结
．
与
之间的大小关系，并证明你的结论；
，求证：
．
中，
两点在边
上，且四边形
是平行四边形．
与
时，求证：平行四边形