初中数学圆内接四边形的性质解答题

已知∠MAN=135°，正方形ABCD绕点A旋转．
（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．
①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是                   ；
②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；
（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．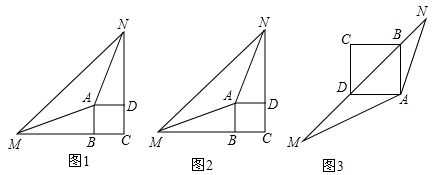

如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5，且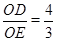，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=－+c经过点E，且与AB边相交于点F．

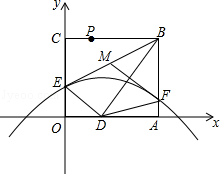
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．

如图，在矩形ABCD中，AD=8，AB=6，点M是BC的中点，点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动，在点P，Q的运动过程中，以PQ为边作正方形PQEF，使它与矩形ABCD在BC的同侧，点P，Q同时出发，当点P返回点M时停止运动，点Q也随之停止，设点P，Q运动的时间是t秒（t＞0）

（1）用含t的代数式表示线段BQ的长；
（2）设正方形PQEF与矩形ABCD重叠部分的面积为S，求S与t之间的函数关系式；
（3）连接AC，当正方形PQEF与△ADC重叠部分为三角形时，直接写出t的取值范围．

如图，矩形ABCD，E是AB上一点，且DE=AB，过C作CF⊥DE于F．

（1）猜想：AD与CF的大小关系；
（2）请证明上面的结论．

如图，矩形ABCD中，E为BC上一点，DF⊥AE于F．

（1）ΔABE与ΔADF相似吗？请说明理由．
（2）若AB=6，AD=12，BE=8，求FD的长．

如图，点E，F分别在正方形ABCD的边DA，DC延长线上，且AE﹣CF，连接BE，BF，过点E作EG∥BF，过点F作FG∥BE，EG，FG交于点G．
（1）求证：△ABE≌△CBF；
（2）求证：四边形BEGF是菱形；
（3）若AD=3AE=3，求四边形BEGF的周长．

如图，已知四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接DE，BF．求证：四边形DEBF是平行四边形．

（如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．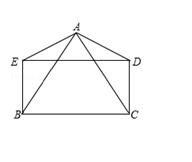

求证：四边形BCDE是矩形．

如图，在平行四边形ABCD中，点E、F分别在BC、AD上，且DF=BE．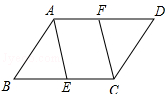

求证：AE=CF．

如图，在正方形ABCD中，CE⊥DF，求证：CE=DF．

如图，四边形ABCD是菱形，CE⊥AB，垂足为点E，且CE交对角线BD于点F．若∠A=120°，四边形AEFD的面积为，求EF的值．

如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4；

（1）求证：四边形ACED是平行四边形
（2）求四边形ACEB的周长．

如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．

（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4，求四边形AEDF的周长．

如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．

（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求△BDE的面积．

已知▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD、AB于E、F，求证：AE=CF．