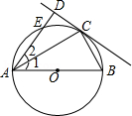
如图,AB为⊙O的直径,点E在⊙O上,C为 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2, ,求AB的长.
已知点 , 和直线 ,则点 到直线 的距离证明可用公式 计算.
例如:求点 到直线 的距离.
解:因为直线 ,其中 , .
所以点 到直线 的距离为: .
根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)已知 的圆心 坐标为 ,半径 为2,判断 与直线 的位置关系并说明理由;
(3)已知直线 与 平行,求这两条直线之间的距离.
已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离B.相切C.相交D.无法确定
如图,直角坐标系中,以5为半径的动圆的圆心 沿 轴移动,当 与直线 只有一个公共点时,点 的坐标为
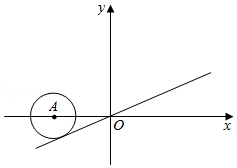
| A. |
|
B. |
|
C. |
|
D. |
|
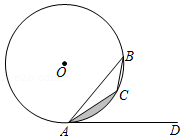
如图,是
的弦,
是
外一点,
,
交
于点
,交
于点
,且
.
(1)判断直线与
的位置关系,并说明理由;
(2)若,
,求图中阴影部分的面积.
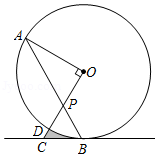
如图,直线 经过 上的点 , 为 的内接三角形,并且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , 的半径为1,求图中阴影部分的面积.(结果保留
如图,在 中, , 平分 交 于点 ,过点 和点 的圆,圆心 在线段 上, 交 于点 ,交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.
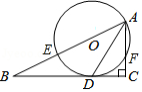
如图,已知 为 的直径,点 在 上, 的平分线交 于点 ,过点 作 的垂线,垂足为 ,直线 与 的延长线交于点 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求线段 的长.

如图,在平面直角坐标系中,与
轴的正半轴交于
、
两点,与
轴的正半轴相切于点
,连接
、
,已知
半径为2,
,双曲线
经过圆心
.
(1)求双曲线的解析式;
(2)求直线的解析式.

已知 的半径为 ,圆心 到直线 的距离为 ,则直线 与 的位置关系为
A.相交B.相切C.相离D.无法确定
已知平面内有 和点 , ,若 半径为 ,线段 , ,则直线 与 的位置关系为
| A. |
相离 |
B. |
相交 |
C. |
相切 |
D. |
相交或相切 |
如图,矩形 中, 是 的中点,过 、 、 三点的圆 与边 、 分别交于点 、点 ,给出下列说法:(1) 与 的交点是圆 的圆心;(2) 与 的交点是圆 的圆心;(3) 与圆 相切,其中正确说法的个数是

A.0B.1C.2D.3
如图, 中, , 为 的平分线,以 上一点 为圆心的半圆经过 、 两点,交 于 ,连接 交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.

试题篮
()