如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是 .
如图,在 中, 为直径, 为弦.过 延长线上一点 ,作 于点 ,交 于点 ,交 于点 , 是 的中点,连接 , .
(1)判断 与 的位置关系,并说明理由;
(2)若 , , ,求 的长.

已知平面内有 和点 , ,若 半径为 ,线段 , ,则直线 与 的位置关系为
| A. |
相离 |
B. |
相交 |
C. |
相切 |
D. |
相交或相切 |
我们把方程 称为圆心为 、半径长为 的圆的标准方程.例如,圆心为 、半径长为3的圆的标准方程是 .在平面直角坐标系中, 与轴交于点 , ,且点 的坐标为 ,与 轴相切于点 ,过点 , , 的抛物线的顶点为 .
(1)求 的标准方程;
(2)试判断直线 与 的位置关系,并说明理由.

如图,点 的坐标是 , ,点 是以 为直径的 上一动点,点 关于点 的对称点为 .当点 在 上运动时,所有这样的点 组成的图形与直线 有且只有一个公共点,则 的值等于 .

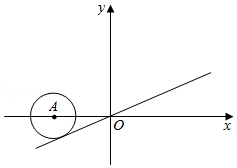
如图,直角坐标系中,以5为半径的动圆的圆心 沿 轴移动,当 与直线 只有一个公共点时,点 的坐标为
| A. |
|
B. |
|
C. |
|
D. |
|
已知平面直角坐标系中,点 , 和直线 (其中 , 不全为 ,则点 到直线 的距离 可用公式 来计算.
例如:求点 到直线 的距离,因为直线 可化为 ,其中 , , ,所以点 到直线 的距离为: .
根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)在(1)的条件下, 的半径 ,判断 与直线 的位置关系,若相交,设其弦长为 ,求 的值;若不相交,说明理由.
如图,已知 为 的直径,点 在 上, 的平分线交 于点 ,过点 作 的垂线,垂足为 ,直线 与 的延长线交于点 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求线段 的长.

在矩形 中, , ,点 在对角线 上,圆 的半径为2,如果圆 与矩形 的各边都没有公共点,那么线段 长的取值范围是 .
如图,在 中, ,点 在 上,以 为半径的 交 于点 , 的垂直平分线交 于点 ,交 于点 ,连接 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , , ,求线段 的长.
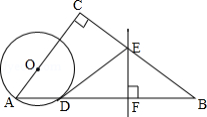
如图, 中, , 为 的平分线,以 上一点 为圆心的半圆经过 、 两点,交 于 ,连接 交 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,求 的长.

阅读材料:
在平面直角坐标系 中, 点 , 到直线 的距离公式为: .
例如: 求点 到直线 的距离 .
解: 由直线 知, , , ,
点 到直线 的距离为 .
根据以上材料, 解决下列问题:
问题 1 :点 到直线 的距离为 ;
问题 2 :已知: 是以点 为圆心, 1 为半径的圆, 与直线 相切, 求实数 的值;
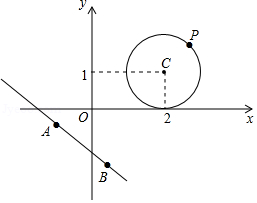
问题 3 :如图, 设点 为问题 2 中 上的任意一点, 点 , 为直线 上的两点, 且 ,请求出 的最大值和最小值 .
试题篮
()