如图,在 中,直径
中,直径 垂直于不过圆心
垂直于不过圆心 的弦
的弦 ,垂足为点
,垂足为点 ,连接
,连接 ,点
,点 在
在 上,且
上,且
(1)求证: ;
;
(2)过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 ,试判断
,试判断 与
与 是否相等,并说明理由;
是否相等,并说明理由;
(3)设 半径为4,点
半径为4,点 为
为 中点,点
中点,点 在
在 上,求线段
上,求线段 的最小值.
的最小值.

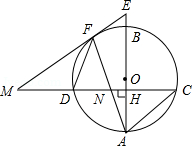
如图,已知 是圆 的直径,弦 ,垂足为 ,与 平行的圆 的一条切线交 的延长线于点 ,交 的延长线于点 ,切点为 ,连接 交 于点 .
(1)求证: ;
(2)连接 ,若 , ,求圆 的直径的长度.
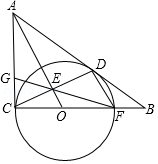
如图, 与 的直角边 和斜边 分别相切于点 、 ,与边 相交于点 , 与 相交于点 ,连接 并延长交 边于点 .
(1)求证: ;
(2)若 , ,求 的长.
如图,以 为直径的 外接于 ,过 点的切线 与 的延长线交于点 , 的平分线分别交 , 于点 , ,其中 , 的长是一元二次方程 的两个实数根.
(1)求证: ;
(2)在线段 上是否存在一点 ,使得四边形 是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
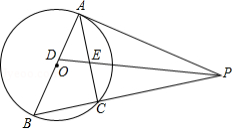
如图, 是 的直径,点 在 上, 的延长线与过点 的切线交于点 , 为线段 上的点,过点 的弦 于点 .
(1)求证: ;
(2)已知 , ,且 ,求 的长.

如图, 是 的直径, 为 上一点, 和过点 的切线互相垂直,垂足为 .
(1)求证: ;
(2)若 , ,求 的长.

如图, 是 的直径, 与 相切于点 ,与 的延长线交于点 , 于点 .
(1)求证: ;
(2)若 , ,求 的半径.

如图,已知 、 为 的两条直径, 为切线,过 上一点 作 于 ,连接 并延长交 于点 ,连接 .
(1)求证: .
(2)设 为点 关于 对称点,连接 、 ,如果 , 的半径为3,求 的值.

如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

如图, 是 的直径,点 为线段 上一点(不与 , 重合),作 ,交 于点 ,作直径 ,过点 的切线交 的延长线于点 ,作 于点 ,连接 .
(1)求证: 平分 ;
(2)求证: ;
(3)当 且 时,求劣弧 的长度.

如图,点 在 外, 是 的切线, 为切点,直线 与 相交于点 、 .
(1)若 ,求证: ;
(2)小明发现, 在一定范围内变化时,始终有 成立.请你写出推理过程.

如图,已知 是 的直径,点 是 上一点,连接 ,点 关于 的对称点 恰好落在 上.
(1)求证: ;
(2)过点 作 的切线 ,交 的延长线于点 .如果 , ,求 的直径.

如图, 为 的内接三角形, 为 的直径,过点 作 的切线交 的延长线于点 .
(1)求证: ;
(2)过点 作 的切线 交 于点 ,求证: ;
(3)若点 为直径 下方半圆的中点,连接 交 于点 ,且 , ,求 的长.
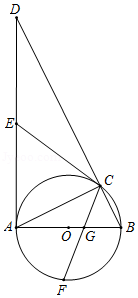
已知 为 的直径, 为 的切线,切点为 ,分别过 , 两点作 的垂线,垂足分别为 , , 的延长线与 相交于点 .
(1)求证: ;
(2)若 , ,求 的长.

试题篮
()