尺规作图(只保留作图痕迹,不要求写出作法).如图,已知 ,且 .
(1)在 边上求作点 ,使 ;
(2)在 边上求作点 ,使 .

在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知 , 是弦 上一点,请你根据以下步骤完成这个引理的作图过程.
(1)尺规作图(保留作图痕迹,不写作法);
①作线段 的垂直平分线 ,分别交 于点 , 于点 ,连接 , ;
②以点 为圆心, 长为半径作弧,交 于点 , 两点不重合),连接 , , .
(2)直接写出引理的结论:线段 , 的数量关系.

如图,已知线段 , ,垂足为 .
(1)求作四边形 ,使得点 , 分别在射线 , 上,且 , , ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)设 , 分别为(1)中四边形 的边 , 的中点,求证:直线 , , 相交于同一点.

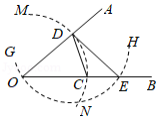
如图,已知Rt△ABC和Rt△EBC, °。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
(1)用尺规确定并标出圆心O;(不写做法和证明,保留作图痕迹)
(2)求证:
 [(3)若AD=1cm,
[(3)若AD=1cm, ,求BC长。
,求BC长。
尺规作图(要求保留作图痕迹):已知:线段a,b. 求作:线段c,使得c=2b-a.

如图,已知 是 外一点.用两种不同的方法过点 作 的一条切线.
要求:(1)用直尺和圆规作图;
(2)保留作图的痕迹,写出必要的文字说明.

如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

如图,已知 中, .
(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).
①作 的角平分线 ,交 于点 ;
②作线段 的垂直平分线 与 相交于点 ;
③以点 为圆心,以 长为半径画圆,交边 于点 .
(2)在(1)的条件下,求证: 是 的切线;
(3)若 , ,求 的半径.

如图,在等腰 中, , ,按下列步骤作图:
①以点 为圆心,适当的长度为半径作弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径作弧相交于点 ,作射线 ;
②分别以点 , 为圆心,大于 的长为半径作弧相交于点 , ,作直线 ,交射线 于点 ;
③以点 为圆心,线段 长为半径作圆.
则 的半径为

A. B.10C.4D.5
已知锐角 ,如图,按下列步骤作图:①在 边取一点 ,以 为圆心, 长为半径画 ,交 于点 ,连接 .②以 为圆心, 长为半径画 ,交 于点 ,连接 .则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 为线段 外一点.
(1)求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的四边形 中, , 相交于点 , , 的中点分别为 , ,求证: , , 三点在同一条直线上.

如图,在 中, ,分别以点 、 为圆心,以大于 的长为半径画弧,两弧分别交于点 、 ,作直线 交 点 ;以点 为圆心,适当长为半径画弧,分别交 、 于点 、 ,再分别以点 、 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 ,此时射线 恰好经过点 ,则 度.

已知线段 ,按如下步骤作图:①作射线 ,使 ;②作 的平分线 ;③以点 为圆心, 长为半径作弧,交 于点 ;④过点 作 于点 ,则

| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()