初中数学平行线分线段成比例试题

已知反比例函数的图象通过点（，），则当时，       ．

若反比例函数的图象经过点（-2，3），则该反比例函数图象一定经过点（ ）

A．（2，-3）

B．（-2，-3）

C．（2，3）

D．（-1，-6）

如图，点P、Q是反比例函数y=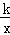图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作PM⊥x轴于点M，QB⊥y轴于点B，连接PB、QM，△ABP的面积记为S₁，△QMN的面积记为S₂，则S₁     S₂．（填“＞”或“＜”或“=”）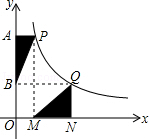
 

如图，O是坐标原点，菱形OABC的顶点A的坐标为（﹣3，4），顶点C在x轴的负半轴上，函数y=（x＜0）的图象经过顶点B，则k的值为（ ）

A．-12

B．-27

C．-32

D．-36

已知反比例函数经过点（1，5），则k=     ．

在第一象限内，点P（2，3），M（a，2）是双曲线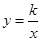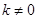（）上的两点，PA⊥x轴于点A，MB⊥x轴于点B，PA与OM交于点C，则△OAC的面积为    ．

若A（－1，y₁）、B（－2，y₂）是反比例函数y＝（m为常数，m≠）图象上的两点，且y₁＞y₂，则m的取值范围是             ．

如图1，点A（8，1）、B（n，8）都在反比例函数（x＞0）的图象上，过点A作AC⊥x轴于C，过点B作BD⊥y轴于D．

（1）求m的值和直线AB的函数关系式；
（2）动点P从O点出发，以每秒2个单位长度的速度沿折线OD﹣DB向B点运动，同时动点Q从O点出发，以每秒1个单位长度的速度沿折线OC向C点运动，当动点P运动到D时，点Q也停止运动，设运动的时间为t秒．
①设△OPQ的面积为S，写出S与t的函数关系式；
②如图2，当的P在线段OD上运动时，如果作△OPQ关于直线PQ的对称图形△O′PQ，是否存在某时刻t，使得点Q′恰好落在反比例函数的图象上？若存在，求Q′的坐标和t的值；若不存在，请说明理由．

如图，双曲线与直线交于A、B两点，且A（﹣2，m），则点B的坐标是（ ）

A．（2，﹣1）      B．（1，﹣2）      C．（，﹣1）      D．（﹣1，）

已知点A（1，y₁）、B（2，y₂）、C（-3，y₃）都在反比例函数y＝的图象上，则y₁、y₂、y₃的大小关系是（  ）

A．y3＜y1＜y2

B．y1＜y2＜y3

C．y2＜y1＜y3

D．y3＜y2＜y1

正比例函数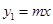（m＞0）的图象与反比例函数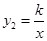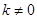（）的图象交于点A(n,4)和点B,AMy轴，垂足为M,若△ABM的面积为8，则满足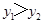的实数x的取值范围是          ．

若双曲线过点（2，6），则该双曲线一定过点（   ）

A．（―3，―4）

B．（4，―3）

C．（―6，2）

D．（4，4）

如图中的曲线是反比例函数y=图象的一支，则m的取值范围是（ ）

A．m＞-5

B．0＜m＜5

C．-5＜m＜0

D．m＜-5

定义新运算：a⊕b=例如：4⊕5=，4⊕（-5）=－．则函数y=2⊕x（x≠0）的图象大致是（ ）

在同一直角坐标系中，函数y =" kx" - k与（k≠0） 的图象大致是 （     ）