初中数学平行线分线段成比例试题

如图，菱形OABC的顶点O是原点，顶点B在y轴上，菱形的两条对角线的长分别是6和4，反比例函数 的图象经过点C，则k的值为            ．

如果点A（-3，y₁），B（-2，y₂），C（1，y₃）都在反比例函数（k>0）的图象上，那么，y₁，y₂，y₃的大小关系是（   ）

A．	B．
C．	D．

如图，在平面直角坐标系xOy中，点，在反比例函数（m为常数）的图象G上，连接AO并延长与图象G的另一个交点为点C，过点A的直线l与x轴的交点为点，过点C作CE∥x轴交直线l于点E．

（1）求m的值及直线l对应的函数表达式；
（2）求点E的坐标；
（3）求证：∠BAE=∠ACB．

已知点A（1，y₁）、B（2，y₂）、C（﹣3，y₃）都在反比例函数的图象上，则y₁、y₂、y₃的大小关系是（ ）

A．y3＜y1＜y2

B．y1＜y2＜y3

C．y2＜y1＜y3

D．y3＜y2＜y1

在反比例函数y=的图象的每一条曲线上，y都随x的增大而增大，写出一个符合题意的k的值         。

在同一直角坐标系中，若正比例函数y=k₁x的图像与反比例函数的图像没有公共点，则（   ）

A．k1+ k2＞0

B．k1+ k2＜0

C．k1k2＞0

D．k1k2＜0

对于反比例函数y=，下列说法不正确的是（ ）

A．点（-2，-1）在它的图像上

B．它的图象在第一、三象限

C．当x>0时，y随x的增大而增大

D．当x<0时，y随x的增大而减小

如图，反比例函数的图象与经过原点的直线 相交于A、B两点，已知A点坐标为，那么B点的坐标为     ．

下列四个点中，有三个点在同一反比例函数的图象上，则不在这个函数图象上的点是 （  ）

A．（5，1）

B．（－1，5）

C．（，3）

D．（－3，）

某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．当气球内的气压大于120 kPa时，气球将爆炸．为了安全起见，气球的体积应 （       ）

A．不小于m^3

B．小于m^3

C．不小于m^3

D．小于m^3

在反比例函数的图象的每一条曲线上，的增大而增大，则的值可以是（   ）

A．

B．0

C．1

D．2

若反比例函数的图像经过，则该函数的图像不经过的点是（  ）

A．

B．

C．

D．

在反比例函数的图像上有两点A（）,B（），当时，有，则m的取值范围是（   ）

A．m＜0

B．m＞0

C．

D．

已知点P(1，-2a)在二次函数y=ax²+6的图象上，并且点P关于x轴的对称点在反比例函数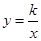的图象上。
（1）求此二次函数和反比例函数的解析式；
（2）点（-1，4）是否同时在（1）中的两个函数图象上？

若当时，正比例函数与反比例函数的值相等，则与的比是（  ）。

A．9:1

B．3:1

C．1:3

D．1:9