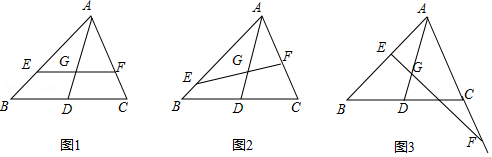
在中,已知
是
边的中点,
是
的重心,过
点的直线分别交
、
于点
、
.
(1)如图1,当时,求证:
;
(2)如图2,当和
不平行,且点
、
分别在线段
、
上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点在
的延长线上或点
在
的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
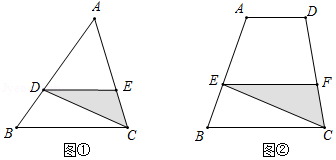
问题1:如图①,在 中, , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 的面积为 , 的面积为 .
(1)当 时, ;
(2)设 ,请你用含字母 的代数式表示 .
问题2:如图②,在四边形 中, , , , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 ,四边形 的面积为 , 的面积为 .请你利用问题1的解法或结论,用含字母 的代数式表示 .
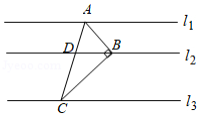
如图,直线,
,
,
分别为直线
,
,
上的动点,连接
,
,
,线段
交直线
于点
.设直线
,
之间的距离为
,直线
,
之间的距离为
,若
,
,且
,则
的最大值为 .
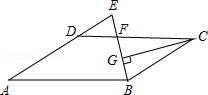
如图,在 中, , , 的平分线交 于点 ,交 的延长线于点 , ,垂足为 ,若 ,则线段 的长为
A. B. C. D.
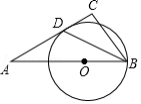
如图, 中, ,点 是边 上一点,以点 为圆心,以 为半径作圆, 恰好与 相切于点 ,连接 .若 平分 , ,则线段 的长是
| A. |
2 |
B. |
|
C. |
|
D. |
|
在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.
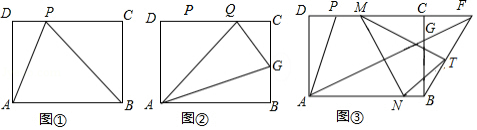
(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
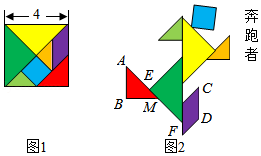
小丽在"红色研学"活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的"奔跑者"形象来激励自己.已知图1正方形纸片的边长为4,图2中 ,则"奔跑者"两脚之间的跨度,即 , 之间的距离是 .
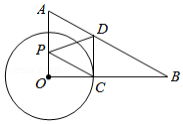
如图,在 中, , , ,以点 为圆心,2为半径的圆与 交于点 ,过点 作 交 于点 ,点 是边 上的动点.当 最小时, 的长为
A. B. C.1D.
如图, 中, , , ,将 绕点 顺时针旋转 得到△ , 为线段 上的动点, 以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为 .
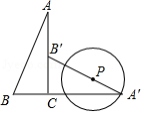
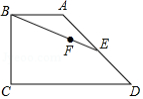
如图,四边形 中, , , , , 为 的中点, 为线段 上的点,且 ,则点 到边 的距离是
A.3B. C.4D.
如图, 的面积为 .点 , , , , 是边 的 等分点 ,且 为整数),点 , 分别在边 , 上,且 ,连接 , , , , ,连接 , , , , ,线段 与 相交于点 ,线段 与 相交于点 ,线段 与 相交于点 , ,线段 与 相交于点 ,则△ ,△ ,△ , ,△ 的面积和是 .(用含有 与 的式子表示)

试题篮
()