初中数学平行线分线段成比例解答题

如图，已知反比例函数y＝过点P， P点的坐标为（3－m，2m），m是分式方程的解，PA⊥x轴于点A，PB⊥y轴于点B.
（1）试判断四边形PAOB的形状，并说明理由．

（2）连结AB，E为AB上的一点，EF⊥BP于点F，G为AE的中点，连结OG、FG，试问FG和OG有何数量关系？请写出你的结论并证明.

（3）若M为反比例函数y＝在第三象限内的一动点，过M作MN⊥x轴于交AB的延长线于点N，是否存在一点M使得四边形OMNB为等腰梯形？若存在，请求出M点的坐标；若不存在，请说明理由.

一司机驾驶汽车从甲地去乙地，以80千米/小时的平均速度用6小时到达目的地.
（1）当他按原路匀速返回时，求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式；
（2）如果该司机匀速返回时，用了4.8小时，求返回时的速度；
（3）若返回时，司机全程走高速公路，且匀速行驶，根据规定：最高车速不得超过每小时120公里，最低车速不得低于每小时60公里，试问返程时间的范围是多少？

已知双曲线经过△AEO的顶点A,且AE=AO=5,,直线与双曲线相交于A, F两点,且F点的坐标为(6,)
（1）求出反比例函数与一次函数的解析式；
（2）连接EF,求△AEF的面积.

若一次数和反比例函数的图象都经过点C(1，1)．
（1）求一次函数的表达式；
（2）已知点A在第三象限，且同时在两个函数图象上，求点A的坐标．

已知反比例函数图象过第二象限内的点A（—2，m）AB⊥x轴于B，Rt△AOB面积为3, 若直线y=ax+b经过点A，并且经过反比例函数的图象上另一点C（n，—1）。

（1）求反比例函数的解析式及m、n的值；
（2）求直线y=ax+b的解析式．

已知当压力不变时，木板对地面的压强p(Pa)是木板面积S（m²）的反比例函数，其图象如图所示.
（1）请直接写出p与S之间的关系式和自变量S的取值范围；
（2）当木板面积为2 m²时，压强是多少？

如图，已知直线y =－x＋4与反比例函数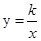的图象相交于点A（-2，a），并且与x轴相交于点B。

（1）求a的值；
（2）求反比例函数的表达式；
（3）求△AOB的面积。

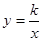正比例函数和反比例函数的图象相交于A，B两点，已知点A的横坐标为1，纵坐标为．

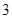（1）写出这两个函数的表达式；
（2）求B点的坐标；
（3）在同一坐标系中，画出这两个函数的图象．

如图，反比例函数y=的图象过矩形OABC的顶点B，OA、0C分别在x轴、y轴的正半轴上，OA：0C=2：1。
（1）求B点的坐标；
（2）若直线y=2x+m平分矩形OABC面积，求m的值。

为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量（mg）与燃烧时间（分钟）成正比例；燃烧后，与成反比例（如图所示）．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．据以上信息解答下列问题：
（1）求室内每立方米空气中的含药量与的函数关系式；
（2）当每立方米空气中含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，经多长时间学生才可以回教室？
（3）经医学论证，只有当每立方米空气中的含药量不低于4mg且持续的时间不少于12分钟时，才认为消毒有效，请问本次消毒有效么？请说明理由。

已知一次函数y=kx+k的图象与反比例函数y=的图像在第二象限交于点B(4,n),(1)求n的值  （2）求一次函数的解析式.

.如图，在直角坐标系中，点A是反比例函数y₁=的图象上一点，AB⊥x轴的正半轴于点B，C是OB的中点，一次函数y₂=ax+b的图象经过A、C两点，并交y轴于点D(0,－2)，若S_{△AO D}=4

（1）求反比例函数和一次函数解析式。
（2）观察图象，请指出在y轴的右侧，当y₁＞y₂时x 的取值范围

已知：△中，边的长为（），上的高为（）.设△中边的长为（），上的高为（）.
（1）求关于的函数解析式和自变量的取值范围；
（2）求当时的取值范围.

如图，四边形ABCD为菱形,已知A(0,4)，B(－3,0).

（1）求点D的坐标；
（2）求经过点C的反比例函数解析式.

如图，直线y=kx+b与反比例函数只有一个交点A（1 , 2）,且与x轴、y轴分别交于B,C两点，AD垂直平分OB，垂足为D，

（1）求点B的坐标和m的值；
（2）求直线解析式