初中数学平行线分线段成比例解答题

你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细（横截面积）xx(mm²)的反比例函数，其图像如上图所示．
写出y与x的函数关系式
若当面条的粗细应不小于1.6mm2，面条的总长度最长是多少？

如图，直线分别交轴，轴于点，点是直线与双曲线在第一象限内的交点，轴，垂足为点，的面积为4．

（1）求点的坐标；
（2）求双曲线的解析式及直线与双曲线另一交点的坐标．

如图，已知反比例函数的图像和一次函数y=kx-7的图像都经过点P(m,2)．
求这个一次函数的解析式
如果等腰梯形ABCD的顶点A、B在这个一次函数的图像上，顶点C、D在这个反比例函数的图像上，两底AD、BC与y轴平行，且A和B的横坐标分别为a、b（b>a>0）,求代数式ab的值．

在平面直角坐标系xOy中，若一次函数的图象与反比例函数的图象相交于A（1， 2）、B（－2，m）两点．
求反比例函数和一次函数的解析式
在所给的坐标系中，画出这个一次函数及反比例函数图象（可以不列表），并直接写出当为何值时，一次函数的值大于反比例函数的值．

已知反比例函数y＝(m为常数)的图象经过点A（－1，6）
．
求m的值
如图，过点A作直线AC与函数y＝的图象交于点B，与x轴交于点C，且AB＝2BC，求点C的坐标

已知反比例函数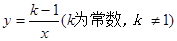
（1）若点A（1，2）在这个函数的图像上，求k的值；
（2）若在这个函数图像的每一分支上，y随x的增大而减小，求k的取值范围；
（3）若k=13，试判断点B（3，4），C（2，5）是否在这个函数的图像上，并说明理由。

如图，已知A(，-2)，B(1，4)是一次函数的图象和反比例函数y=的图象的两个交点，直线AB与轴交于点C．.

求反比例函数和一次函数的关系式；
求△AOC的面积
观察图象，直接写出不等式＜0的解集.

如图，一次函数的图象与反比例函数的图象相交于点A、B．
求：(1) 求反比例函数和一次函数的解析式．

(2) 求直线AB与x轴的交点C的坐标及的面积．
(3) 直接写出一次函数的值大于反比例函数的值的x的取值范围．

正比例函数y＝x的图象与反比例函数y＝的图象的一个交点纵坐标是2.
求m的值
当－3＜x＜－1时,求反比例函数y的取值范围

如图，在平面直角坐标系中，函数的图象经过点A(3，2)和B(，)，过点A作y轴的垂线，垂足为C．

求的值；
当△ABC的面积为时，求直线AB的解析式．

已知一次函数的图像经过点A(1，0)和B（），且点B在反比例函数的图像上．
求一次函数的解析式；
若点M是轴上一点，且满足△ABM是直角三角形，请直接写出点M的坐标．

探究  
在图1中，已知线段AB，CD，其中点分别为E，F．
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；

归纳
①在图2中，已知线段AB的端点坐标为A(1，1) ，B(3，3)，
则AB 的中点C的坐标__________
②无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为
A(a，b)，B(c，d)， AB中点C的坐标为______

运用 
在图3中，一次函数与反比例函数的图象交点为A（-1，-3），B（3 , n）．

①求出m、n的值；
②求出一次函数的表达式；
③若四边形AOBP为平行四边形,请利用上面的结论求出顶点P的坐标．

直线y=k₁x+b与双曲线y=只有—个交点A(1，2)，且与x轴、y轴分别交于B,C 两点，AD垂直平分OB，垂足为D，求直线、双曲线的解析式．

如图一次函数（）的图象分别交轴、轴于点，与反比例函数图象在第二象限交于点，轴于点，OA＝OD．
求m的值和一次函数的表达式；
在轴上求点，使△CAP为等腰三角形（求出所有符合条件的点）

如图，已知反比例函数的图象经过点(，8)，直线经过该反比例函数图象上的点Q(4，)．

求上述反比例函数和直线的函数表达式；
设该直线与轴、轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．