如图,直线y=k1x+b与反比例函数y= (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值.
(2)直接写出k1x+b﹣ >0时x的取值范围;
>0时x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
如图,直线 分别交
分别交 轴、
轴、 轴于A、C两点,且与双曲线
轴于A、C两点,且与双曲线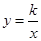 在第一象限交于点P,作PB⊥
在第一象限交于点P,作PB⊥ 轴于B,
轴于B, .
.
(1)直接写出点A、C的坐标;
(2)求双曲线的函数式
假期里,小红和小慧去买菜,三次购买的西红柿价格和数量如下表:
| 单价/(元/千克) |
4 |
3 |
2 |
合计 |
| 小红购买的数量/千克 |
1 |
2 |
3 |
6 |
| 小慧购买的数量/千克 |
2 |
2 |
2 |
6 |
(1)小红和小慧购买西红柿数量的中位数是2,众数是2;
(2)从平均价格看,谁买的西红柿要便宜些.
小亮的说法
每次购买单价相同,购买总量也相同,平均价格应该也一样,都是(4+3+2)÷3=3(元/千克),所以两人购买的西红柿一样便宜.
小明的说法
购买的总量虽然相同,但小红花了16元,小慧花了18元,平均价格不一样,所以购买的西红柿便宜
思考小亮和小明的说法,你认为谁说得对?为什么?
(3)小明在直角坐标系中画出反比例函数的图象,图象经过点P(如图),点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数.
①求此反比例函数的关系式;
②判断点Q(2,5)是否在此函数图象上.
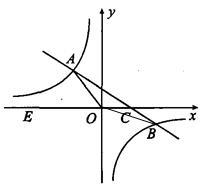
如图在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=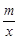 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=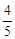 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式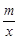 ﹤kx+b的x的取值范围.
﹤kx+b的x的取值范围.
A,B两地相距400km,甲车从A地出发,以60km/h的速度匀速行驶到B地,设甲车与B的路程为y(km),行驶的时间为x(h),求y关于x的函数解析式,并写出自变量x的取值范围.
已知反比例函数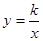 经过点(l,2).
经过点(l,2).
(1)求k的值;
(2)若反比例函数的图象经过点P(a,a-1),求a的值.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
如图,在 中, , , , 为 边上的动点(与 、 不重合), ,交 于点 ,连接 ,设 , 的面积为 .
(1)用含 的代数式表示 的长;
(2)求 与 的函数表达式,并求当 随 增大而减小时 的取值范围.

如图,矩形ABCD的顶点A、B分别在x轴、y轴上,AD=2AB,直线AB的解析式为y=-2x+4,双曲线y= (x>0)经过点D,与BC边相交于点E.
(x>0)经过点D,与BC边相交于点E.

(1)填空:k=
(2)连接AE、DE,试求△ADE的面积;
(3)在x轴上是否存在点P,使得△PCD的周长最小?若存在,求出点P坐标及此时△PCD周长的最小值;若不存在,请说明理由.
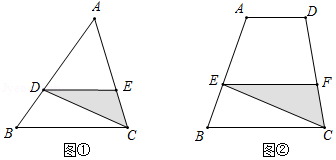
问题1:如图①,在 中, , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 的面积为 , 的面积为 .
(1)当 时, ;
(2)设 ,请你用含字母 的代数式表示 .
问题2:如图②,在四边形 中, , , , 是 上一点(不与 , 重合), ,交 于点 ,连接 .设 ,四边形 的面积为 , 的面积为 .请你利用问题1的解法或结论,用含字母 的代数式表示 .
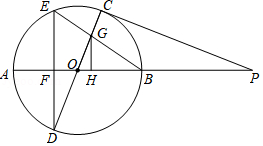
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
如图,在 中, ,点 从点 向点 运动,点 从点 沿射线 方向运动,且 ,连接 交 于 .
(1)如图1,当 时,求证: ;
(2)如图2,当 时,① , ,则 ;
②过点 作 于点 ,探究线段 , , 之间的数量关系,直接写出结论,不需证明.

如图,正方形的边
在正方形
的边
上,连接
,过点
作
,交
于点
.连接
,
,其中
交
于点
.
(1)求证:为等腰直角三角形.
(2)若,
,求
的长.
已知一次函数 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数  (k为常数,
(k为常数, )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点 的坐标;
的坐标;
(2)观察图象,写出使函数值 的自变量
的自变量 的取值范围;
的取值范围;
试题篮
()