如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在轴和轴上,其中OA=6,OC=3.已知反比例函数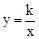 (x>0)的图象经过BC边上的中点D,交AB于点E.
(x>0)的图象经过BC边上的中点D,交AB于点E.
(1)k的值为 ;
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.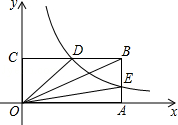
喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
如图,在平面直角坐标系中,双曲线经过点B,连结OB.将OB绕点O按顺时针方向旋转90°并延长至A,使OA=2OB,且点A的坐标为(4,2).
(1)求过点B的双曲线的函数关系式;
(2)根据反比例函数的图像,指出当x<-1时,y的取值范围;
(3)连接AB,在该双曲线上是否存在一点P,使得S△ABP=S△ABO,若存在,求出点P坐标;若不存在,请说明理由.
如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数 的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.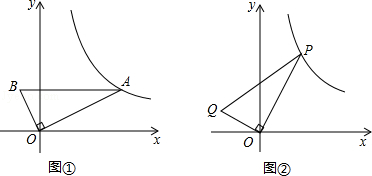
如图,已知A(a,m)、B(2a,n)是反比例函数y= (k>0)与一次函数y=-
(k>0)与一次函数y=- x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?
直线 与双曲线
与双曲线 相交于A、B两点,已知点A(﹣2,﹣1).
相交于A、B两点,已知点A(﹣2,﹣1).
(1)求k的值及点B的坐标;
(2)若点P是y轴正半轴上的动点,判断有几个位置能使△PBO为等腰三角形,直接写出相应的点P的坐标.
已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)在x轴的正半轴上存在一点P,且△ABP的面积是6,请直接写出点P的坐标.
如图,已知反比例函数y= 与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的解析式;
(2)若点D的坐标为(1,0),求△ACD的面积.
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
⑴求k的值;
⑵若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:

⑴把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
⑵观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
⑶当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
⑷当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变).
⑴从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
⑵因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
如图,直线y=x﹣1与反比例函数y= 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
⑴求反比例函数的解析式;
⑵若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
⑶若B(2,1),当x为何值时,一次函数的值大于反比例函数的值
如图,一次函数y=kx+1(k≠0)与反比例函数y=(m≠0)的图象在第一象限有公共点A(1,2).直线l⊥y轴. 于点D(0,3),与反比例函数和一次函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?
试题篮
()