初中数学平行线分线段成比例解答题

如图，点A，B分别在轴，轴上，点D在第一象限内，DC⊥轴于点C，AO=CD=2，AB=DA=，反比例函数的图象过CD的中点E。

（1）求证：△AOB≌△DCA；
（2）求的值；
（3）△BFG和△DCA关于某点成中心对称，其中点F在轴上，试判断点G是否在反比例函数的图象上，并说明理由。（

如图，已知▱ABCD水平放置在平面直角坐标系xOy中，若点A，D的坐标分别为（－2，5），（0，1），点B（3，5）在反比例函数y=（x＞0）图象上．
（1）求反比例函数y=的解析式；
（2）将▱ABCD沿x轴正方向平移10个单位后，能否使点C落在反比例函数y=的图象上？并说明理由．

如图，在平面直角坐标系xOy中，一次函数y=ax+b的图象与x轴相交于点A（-2，0），与y轴交于点C，与反比例函数在第一象限内的图象交于点B（m，n），连结OB．若S_△AOB=6，S_△BOC=2．
（1）求一次函数的表达式；
（2）求反比例函数的表达式．

如图，一次函数y=kx+b（k≠0）的图象过点P（﹣，0），且与反比例函数y=（m≠0）的图象相交于点A（﹣2，1）和点B．
（1）求一次函数和反比例函数的解析式；
（2）求点B的坐标，并根据图象回答：当x在什么范围内取值时，一次函数的函数值小于反比例函数的函数值？

如图，在平面直角坐标系中，Rt△PBD的斜边PB落在y轴上，tan∠BPD=．延长BD交x轴于点C，过点D作DA⊥x轴，垂足为A，OA=4，OB=3．
（1）求点C的坐标；
（2）若点D在反比例函数y=（k＞0）的图象上，求反比例函数的解析式．

下表中，y是x的一次函数．

x	2	1	2		5
y	6	3		12	15

 
（1）求该函数的表达式，并补全表格；
（2）已知该函数图象上一点M（1，-3）也在反比例函数图象上，求这两个函数图象的另一交点N的坐标．

如图，直线y=mx与双曲线y=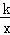相交于A、B两点，A点的坐标为（1，2）
（1）求反比例函数的表达式；
（2）根据图象直接写出当mx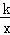＞时，x的取值范围；
（3）计算线段AB的长．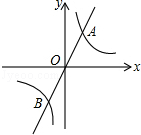

如图，一次函数y=x+b的图象与反比例函数y=（x＞0）的图象交于点A（2，1），与x轴交于点B．
（1）求k和b的值；
（2）连接OA，求△AOB的面积．

如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A（，﹣2），反比例函数y=（x＞0）的图象过点A．
（1）求直线l的解析式；
（2）在函数y=（x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．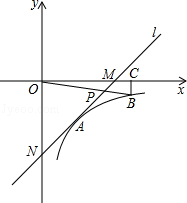

如图，在平面直角坐标系中，一次函数（a为常数）的图象与y轴相交于点A，与函数的图象相交于点B，．
（1）求点B的坐标及一次函数的解析式；
（2）若点P在y轴上，且△PAB为直角三角形，请直接写出点P的坐标．

如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数的图象交于一、三象限的A、B两点，与x轴交于点C．已知，，．    
（1）求反比例函数和一次函数的解析式；
（2）求△OBC的面积．

如图，在平面直角坐标系中，反比例函数的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（-2，4）．
（1）直接写出A、B、D三点的坐标；
（2）若将矩形只向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，求反比例函数的解析式和此时直线AC的解析式y=mx+n．并直接写出满足的x取值范围．

反比例函数在第二象限的图象如图所示.
（1）直接写出m的取值范围；
（2）若一次函数的图象与上述反比例函数图象交于点A，与x轴交于点B，△AOB的面积为，求m的值.

平面直角坐标系中，一次函数和反比例函数的图象都经过点.
（1）求的值和一次函数的表达式；
（2）点B在双曲线上，且位于直线的下方，若点B的横、纵坐标都是整数，直接写出点B的坐标.

如图，已知A（－4，）、B（2，－4）是一次函数的图象和反比例函数的图象的两个交点。
（1）求反比例函数和一次函数的解析式；
（2）求直线AB和轴的交点C的坐标及△AOB的面积；
（3）求方程的解（请直接写出答案）；
（4）求不等式的解集（请直接写出答案）。