初中数学平行线分线段成比例解答题

函数和的图象关于y轴对称，我们定义函数和相互为“影像”函数。
类似地，如果函数和的图象关于y轴对称，那么我们定义函数和互为“影像”函数。
（1）请写出函数的“影像”函数：   ；
（2）函数     的“影像”函数是；
（3）如果，一条直线与一对“影像”函数和的图象分别交于点A、B、C（点A、B在第一象限），如果CB: BA=1:2，点C在函数的“影像”函数上的对应点的横坐标是1，求点B的坐标。

如图，矩形OABC的顶点A、C分别在x轴和y轴上，点的坐标为(2，3)．双曲线的图像经过BC的中点D，且与AB交于点E，连接DE．
（1）求k的值及点E的坐标；
（2）若点F是边上一点，且ΔFCB∽ΔDBE，求直线FB的解析式

如图，一次函数的图象与x轴交于点A，与y轴交于点B，与反比例函数的图象在第一象限内交于点C，CD⊥x轴于点D，OD＝2AO，求反比例函数的表达式．

如图，在平面直角坐标系xOy中，一次函数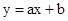的图象与x轴交于点A，与y轴交于点B，已知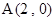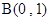，，点C（-2，m）在直线AB上，反比例函数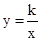的图象经过点C．
（1）求一次函数及反比例函数的解析式；
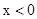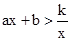（2）结合图象直接写出：当时，不等式的解集．

已知：如图，反比例函数与一次函数的图象交于A（3,1）、B（m，-3）两点.
（1）求反比例函数与一次函数的解析式.
（2）若点P是直线上一点，且OP=OA，请直接写出点P的坐标.

如图，已知等腰△AOB放置在平面直角坐标系xOy中， OA=OB，点B的坐标为(3，4) ．
（1）求直线AB的解析式；
（2）问将等腰△AOB沿x轴正方向平移多少个单位，能使点B落在反比例函数 （x＞0）的图象上．

如图,已知直线与坐标轴相交于A、B两点，与双曲线交于点C．A、D两点关于y轴对称若四边形OBCD的面积为6，求k的值．

许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋转位置从0度到90度（如图），燃气关闭时，燃气灶旋转的位置为0度，旋转角度越大，燃气流量越大，燃气开到最大时，旋转角度为90度．为测试燃气灶旋转在不同位置上的燃气用量，在相同条件下，选择燃气灶旋钮的5个不同位置上分别烧开一壶水（当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90），记录相关数据得到下表：

旋钮角度（度）	20	50	70	80	90
所用燃气量（升）	73	67	83	97	115

 
（1）请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律？说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
（2）当旋钮角度为多少时，烧开一壶水所用燃气量最少？最少是多少？
（3）某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气量．

阅读材料：
若a，b都是非负实数，则a+b≥．当且仅当a=b时，“=”成立．
证明：∵（）²≥0，∴a﹣+b≥0．
∴a+b≥．当且仅当a=b时，“=”成立．
举例应用：
已知x＞0，求函数y=2x+的最小值．
解：y=2x+≥=4．当且仅当2x=，即x=1时，“=”成立．
当x=1时，函数有最小值，y_最小=4．
问题解决：
汽车的经济时速是指汽车最省油的行驶速度．某种汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油（+）升．若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
（1）求y关于x的函数关系式（写出自变量x的取值范围）；
（2）求该汽车的经济时速及经济时速的百公里耗油量（结果保留小数点后一位）．

如图，一次函数y=kx+1（k≠0）与反比例函数y=（m≠0）的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C．

（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积？

如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3）．反比例函数y=（x＞0）的函数图象经过点D，点P是一次函数y=kx+3-3k（k≠0）的图象与该反比例函数图象的一个公共点．

（1）求反比例函数的解析式；
（2）通过计算，说明一次函数y=kx+3-3k（k≠0）的图象一定过点C；
（3）对于一次函数y=kx+3-3k（k≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围（不必写出过程）．

如图，已知反比例函数y₁＝ (k₁＞0)与一次函数y₂＝k₂x＋1(k₂≠0)相交于A、B两点，AC⊥x轴于点C.若△OAC的面积为1，且tan∠AOC＝2.

(1)求出反比例函数与一次函数的解析式；
(2)请直接写出B点的坐标，并指出当x为何值时，反比例函数y₁的值大于一次函数y₂的值？

某乡要在生活垃圾存放区建一个老年活动中心，这样必须把1 200 m³的生活垃圾运走．
(1)假如每天能运x m³，所需时间为y天，写出y与x之间的函数关系式；
(2)若每辆拖拉机一天能运12 m³，则5辆这样的拖拉机要多少天才能运完？
(3)在(2)的情况下，运了8天后，剩下的任务要在不超过6天的时间完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？

如图，一次函数y₁＝kx＋b的图象与反比例函数y₂＝的图象相交于点A(2，3)和点B，与x轴相交于点C(8，0)．

(1)求这两个函数的解析式；
(2)当x取何值时，y₁＞y₂.

如图，已知一次函数与反比例函数的图象交于点A(－4，－2)和B(a，4)．

(1)求反比例函数的解析式和点B的坐标；
(2)根据图象回答，当x在什么范围内时，一次函数的值大于反比例函数的值？