如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.

(1)当点P运动到线段OA的中点时,点C的坐标为 ;
(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;
(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).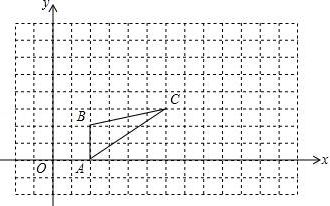
(1)请在图中画出一个△A′B′C′,使△A′B′C′与△ABC是以坐标原点为位似中心,相似比为2的位似图形.
(2)求△A′B′C′的面积.
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,求DE∶EC的值.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C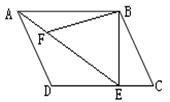
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长;
(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)
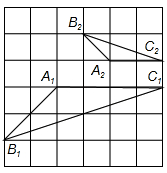
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如上图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”,那么你认为△A1B1C1和△A2B2C2 ,(相似或不相似);理由是 .
如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆A、B,恰好被南岸的两棵树C、D遮住,并且在这两棵树之间还有三棵树,求河的宽度.
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
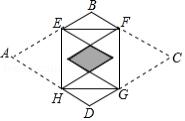
A. B.2C. D.4
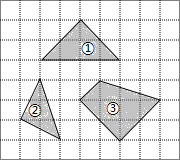
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作▱DEFA.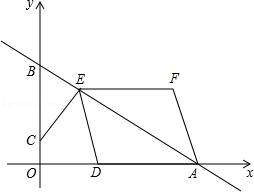
(1)当m=1时,求AE的长.
(2)当0<m<3时,若▱DEFA为矩形,求m的值;
(3)是否存在m的值,使得▱DEFA为菱形?若存在,直接写出m的值;若不存在,请说明理由.
如图,在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积比为 .

试题篮
()