初中数学相似多边形的性质解答题

．
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

（1）求证：△ADF∽△DEC：
（2）若AB=4，AD=3，AE=3，求AF的长．

如图：是7×7的正方形网格，请在所给网格中按下列要求操作：

（1）请在网格中建立平面直角坐标系，使A点坐标为（－4，2），B点坐标为（－2，4）．
（2）在第二象限内格点上找一点C，使C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_________；△ABC周长是____________．（结果保留根号）
（3）画出三角形ABC以O为位似中心，相似比为的位似图形．

（本小题满分10分）如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12．动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．

（1）求梯形ABCD的面积；
（2）当P点离开D点几秒后，PQ//AB；
（3）当P、Q、C三点构成直角三角形时，求点P从点D运动的时间?

（本题12分）
(1)学习《测量建筑物的高度》后，小明带着卷尺、标杆，利用太阳光去测量旗杆的高度．参考示意图1，他的测量方案如下：

第一步，测量数据．测出CD＝1.6米，CF＝1.2米， AE＝9米．
第二步，计算．
请你依据小明的测量方案计算出旗杆的高度．
(2) 如图2，校园内旗杆周围有护栏，下面有底 座．现在有卷尺、 标杆、平面镜、测角仪等工具，请你选择出必须的工具，设计一个测量方案以求出旗杆顶端到地面的距离．要求：在备用图中画出示意图，说明需要测量的数据．(注意不能到达底部点N对完成测量任务的影响，不需计算)你选择出的必须工具是                   ；需要测量的数据是                                        ．

（ 10分）如图，是⊙O的直径，为延长线上的任意一点，为半圆的中点，切⊙O于点，连结交于点．

　　求证：（1）；
（2）．

(8分)(1)学习《测量建筑物的高度》后，小明带着卷尺、标杆，利用太阳光去测量旗杆的高度．
参考示意图1，他的测量方案如下：
第一步，测量数据．测出CD＝1.6米，CF＝1.2米， AE＝9米．
第二步，计算．
请你依据小明的测量方案计算出旗杆的高度．

(2) 如图2，校园内旗杆周围有护栏，下面有底座．现在有卷尺、
标 杆、平面镜、测角仪等
工具，请你选择出必须的工具，设计一个测量方案，以求出旗杆顶端到地面的距离．
要求：在备用图中画出示意图，说明需要测量的数据．(注意不能到达底部点N对完成测量任务的影响，不需计算)
你选择出的必须工具是                   ；
需要测量的数据是                                        ．

如图，抛物线y=ax²+bx+c经过点A（0，4）、B（2，4），它的最高点纵坐标为，点P是第一象限抛物线上一点且PA=PO，过点P的直线分别交射线AB、x正半轴于C、D．设AC=m，OD=n．

（1）求此抛物线的解析式；
（2）求点P的坐标及n关于m的函数关系式；
（3）连结OC交AP于点E，如果以A、C、E为顶点的三角形与△ODP相似，求m的值．

一次函数的图象经过点，且分别与轴、轴交于点、．
点在轴正半轴上运动，点在轴正半轴上运动，且．
(1)求的值，并在给出的平面直角坐标系中画出该一次函数的图象；
(2)求与满足的等量关系式．

(12分)如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．

（1）求抛物线的解析式；
（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；
（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标；若不存在，说明理由．

已知正方形纸片ABCD的边长为2．
操作：如图1，将正方形纸片折叠，使顶点A落在边CD上的点P处(点P与C、D不重合)，折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．

探究：(1)观察操作结果，找到一个与△DEP相似的三角形，并证明你的结论；
(2)当点P位于CD中点时，你找到的三角形与△DEP周长的比是多少？

（本小题满分14分）
在如图所示的一张矩形纸片（）中，将纸片折叠一次，使点与重合，再展开，折痕交边于，交边于，分别连结和．

（1）求证：四边形是菱形；
（2）过作交于，求证：
（3）若，的面积为，求的周长；

如图1，边长为2的正方形ABCD中，E是BA延长线上一点，且AE＝AB，点P从点D
出发，以每秒1个单位长度沿D→C→B向终点B运动，直线EP交AD于点F，过点F作
直线FG⊥DE于点G，交AB于点R。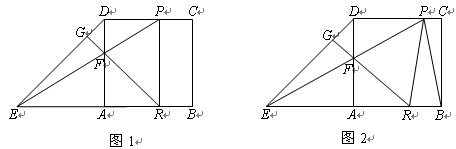

（1）求证：AF＝AR；
（2）设点P运动的时间为t，
①求当t为何值时，四边形PRBC是矩形？
②如图2，连接PB。请直接写出使△PRB是等腰三角形时t的值。

如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿CB方向平移得到的，连结AE，AC和BE相交于点O.

（1）判断四边形ABCE是怎样的四边形，并证明你的结论；
（2）如图2，P是线段BC上一动点（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；
②当线段BP的长为何值时，以点P、Q、R为顶点的三角形与△BOC相似？

如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．

（如果需要，还可以继续操作、实验与测量）
操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．

	PA	PQ
第一次
第二次

 
观测测量结果，猜测它们之间的关系：____________
请证明你猜测的结论；
当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）

(本题8分)如图，在一块三角形区域ABC中，∠C=90°，边AC=8m，BC=6m，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上．

（1）求△ABC中AB边上的高h；
（2）设DG=x，水池DEFG的面积为S，求S关于x的函数关系式，当x取何值时，水池DEFG的面积S最大？