初中数学相似多边形的性质解答题

如图，在平面直角坐标系中，点A，B的坐标分别为A（2，4），B（4，0）.
以原点O为位似中心，把线段AB缩小为原来的；
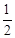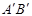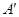若（1）中画出的线段为，请写出线段两个端点,的坐标；
若线段AB上任意一点M的坐标为（a，b），请写出缩小后的线段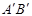上对应点
的坐标．
                                   

已知四边形ABCD的外接圆⊙O的半径为5，对角线AC与BD的交点为E，且AB²=AE·AC，BD=8，

判断△ABD的形状并说明理由；
求△ABD的面积

取一副三角板按图①拼接，固定三角板ADC，将三角板ABC绕点A依顺时针方向旋转一个大小为α的角（0°＜α≤45°得到⊿ABC^/，如图②所示。试问：
当α为多少度时，能使得图②中AB∥CD？
当旋转至图③位置，此时α又为多少度？图③中你能找出哪几对相似三角形，并求其中一对的相似比。
连结BD，当0°＜α≤45°时，探寻∠DBC^/+∠CAC^/+∠BDC值的大小变化情况，并给出你的证明。

如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=8，CD=6，BC = 4，AB边上有一动点P(不与A、B重合)，连结DP，作PQ⊥DP，使得PQ交射线BC于点E，设AP=x．
当x为何值时，△APD是等腰三角形？
若设BE=y，求y关于x的函数关系式
若BC的长可以变化，在现在的条件下，是否存在点P，使得PQ经过点C？若存在，求出相应的AP的长；若不存在，请说明理由，并直接写出当BC的长在什么范围内时，可以存在这样的点P，使得PQ经过点C．
   

如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心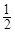，AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．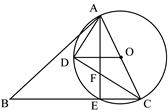

求证：D是弧AE的中点；
求证：∠DAO＝∠B＋∠BAD；
若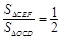，且AC＝4，求CF的长．

在△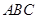中，AD⊥BC，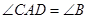

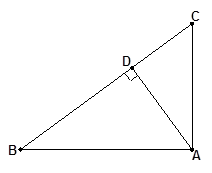
（1）利用尺规作图，作△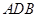外接圆⊙O；
（2）判断：AC和⊙O的位置关系,并说明理由；
（3）若AC=10，AD=8，求⊙O的直径；

如图⊙P的圆心P在⊙O上，⊙O的弦AB所在的直线与⊙P切于C，若⊙P的半径为r，⊙O的半径为R.⊙O和⊙P的面积比为9∶4，且PA=10，PB=4.8，DE=5，C、P、D三点共线

（1）求证：；
（2），求AE的长；
（3）连结PD，求sin∠PDA的值.

如图，四边形ABCD为矩形，AB＝4，AD＝3，动点M、N分别从D、B同时出发，以1个单位/秒的速度运动，点M沿DA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于点P，连结MP。已知动点运动了秒。

请直接写出PN的长           ；（用含的代数式表示）
若0秒≤≤3秒，试求△MPA的面积S与时间秒的函数关系式，并求S的最大值。
若0秒≤≤3秒，△MPA能否与△PCN相似？若能，试求出相似时的对应值；若不能，试说明理由。

等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边AB、AC交于点E、F.（1）如图1，当点P为BC的三等分点，且PE⊥AB时，判断△EPF的形状；

（2）如图2，若点P在BC边上运动，且保持PE⊥AB，设BP=x，四边形AEPF面积的y，求y与x的函数关系式，并写出自变量x的取值范围；
（3）如图3，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长.

如图，以△ABC的边AB为直径的⊙O与边BC交于点D，过点D作DE⊥AC,垂足为E，延长AB、ED交于点F，AD平分∠BAC．（1）求证：EF是⊙O的切线；（2）若AE=3，BF=2，求⊙O的半径．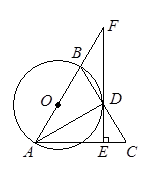

如图①，二次函数的抛物线的顶点坐标C，与x轴的交于A(1,0)、B(-3,0)两点，与y轴交于点D（0,3）
求这个抛物线的解析式
如图②，过点A的直线与抛物线交于点E，交轴于点F，其中点E的横坐标为-2，若直线为抛物线的对称轴，点G为直线上的一动点，则轴上是否存在一点H，使四点所围成的四边形周长最小，若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由；
如图③，连接AC交y轴于M，在x轴上是否存在点P，使以P、C、M为顶点的三角形与△AOM相似？若存在，求出点P的坐标；若不存在，请说明理由.

图①                                     图②

图③

如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．

求证：AD⊥DC
若，，求的值以及AB的长．

如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，D、E分别是边AB、AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR‖BA交AC于R，当点Q与点C重合时，点P停止运动．
求点D到BC的距离DH的长；
设BQ＝x, QR＝y．
① 求y关于x的函数关系式（0≤x≤10）；
② 是否存在点P，使△PQR为等腰三角形？若存在，求出所有满足要求的x的值；若不存在，请说明理由．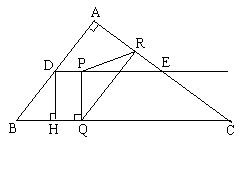

如图，△ABC是等边三角形，点D、E分别在BC、AC上，BD=CE，AD与BE相交于点F．

试说明：△ABD≌△BCE
△AEF与△ABE相似吗?请说明理由．
试说明：BD²=AD·DF

如图，两颗树的高度分别为AB＝6m，CD＝8m，两树的根部间的距离AC＝4m，小强沿着  正对这两棵树的方向从左向右前进，如果小强的眼睛与地面的距离为1.6m，当小强与树AB的距离小于多少时，就不能看到树CD的树顶D？