初中数学相似多边形的性质解答题

如图（1），（2）所示，矩形ABCD的边长AB＝6，BC＝4，点F在DC
上，DF＝2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PQW．设动点M、N的速度都是1个单位／秒，M、N运动的时间为x秒．试解答下列问题：
DM=___▲____,  AN=___▲____（用含x的代数式表示）
说明△FMN ∽ △QWP；
试问为何值时，△PQW为直角三角形？

问当为____▲_____时，线段MN最短？

如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.(1)ΔABE与ΔADF相似吗？请说明理由.(2)若AB=6，AD=12，BE=8，求DF的长.

如图，C为以AB为直径的⊙O上一点，AD和过点C的切线互相垂直，垂足为点D．

（1）求证：AC平分∠BAD；
（2）若CD3，AC=3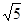，求⊙O的半径长．

在矩形ABCD中，点P在AD上，AB=2，AP=1，将三角板的直角顶点放在点P处，三角板的两直角边分别能与AB、BC边相交于点E、F，连接EF．
（1）如图，当点E与点B重合时，点F恰好与点C重合，求此时PC的长；
（2）将三角板从（1）中的位置开始，绕点P顺时针旋转，当点E与点A重合时停止，在这个过程中，请你观察、探究并解答：
① ∠PEF的大小是否发生变化？请说明理由；
② 直接写出从开始到停止，线段EF的中点所经过的路线长．

如图，在平面直角坐标系中，点C（-3,0），点A、B分别在x轴，y轴的正半轴上，且满足.
求点A、B坐标
若点P从点C出发，以每秒1个单位的速度沿射线CB运动，连接AP。设△ABP面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围
在（2）的条件下，是否存在点P，使以点A、B、P为顶点的三角形与△AOB相似？若存在，请直接写出点P的坐标；若不存在，请说明理由。

在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为（0°＜＜180°），得到△A′B′C．
如图（1），当AB∥CB′时，设A′B′与CB相交于点D．证明：△A′CD是等边三角形；
如图（2），连接A′A、B′B，设△ACA′ 和△BCB′ 的面积分别为S_△ACA′ 和S_△BCB′．求证：S_△ACA′ ：S_△BCB′ =1：3；

如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．

（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若，要使△DEF为等腰三角形，m的值应为多少？

等腰△ABC，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转．

（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE∽△CFP；
（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．
①       探究１：△BPE与△CFP还相似吗？（只需写出结论）
②       探究２：连结EF，△BPE与△PFE是否相似？请说明理由；

正方形边长为4，、分别是、上的两个动点，当点在上运动时，保持和垂直，设MB=x

（1）证明：；
（2）当点运动到什么位置时，
求此时的值．

如图，在平面直角坐标系中，点，点分别在轴，轴的正半轴上，且满足．

求点，点的坐标
若点从点出发，以每秒1个单位的速度沿线段运动，连结．设的面积为，点的运动时间为秒，求与的函数关系式，并写出自变量的取值范围．
在（2）的条件下，是否存在点，使以点为顶点的三角形与相似？若存在，请直接写出点的坐标；若不存在，请说明理由．

如图，在矩形中，点分别在边上，BE⊥EF，

ΔABE与ΔDEF相似吗？请说明理由.
若，求CF的长．

（1）如图①所示，菱形ABCD与等腰△AEF有公共顶点A, AE=AF,∠EAF=∠BAD, 连接BE、DF．
求证：∠ABE =∠ADF．

(2) 如图②所示，将（1）中的菱形ABCD变为平行四边形ABCD，等腰△AEF变为一般△AEF，且AD=kAB,AF=kAE,其他条件不变．(1)中的结论是否还成立？说明理由．

在一个三角形中，如果一个角是另一个角的2倍，我们称这种三角形为倍角三角形．如图1，倍角△ABC中，∠A=2∠B，∠A、∠B、∠C的对边分别记为a,b,c，倍角三角形的三边a,b,c有什么关系呢？让我们一起来探索．

（1）我们先从特殊的倍角三角形入手研究.请你结合图形填空：

三角形	角的已知量
图2	∠A=2∠B=
图3	∠A=2∠B=

（2）如图4，对于一般的倍角△ABC，若∠CAB=2∠CBA ，∠CAB、∠CBA、∠C的对边分别记为a、b、c，a、b、c三边有什么关系呢？请你作出猜测，并结合图4给出的辅助线提示加以证明．

已知：如图1，在平面直角坐标系中，O为坐标原点，直线y＝kx＋b与x轴、y轴分别交与点A、B，与双曲线y＝相交于C、D两点，且点D的坐标为（1，6）.
（1）当点C的横坐标为2时，试求直线AB的解析式，并直接写出的值为    .

（2）如图2，当点A落在x 轴的负半轴时，过点C作x轴的垂线，垂足为E，过点D作y轴的垂线，垂足为F，连接EF.①判断ΔEFC的面积和ΔEFD的面积是否相等，并说明理由；②当＝2时，求tan∠OAB的值.

如图，∠C＝90º，点A、B在∠C的两边上，CA＝30，CB＝20，连接AB．点P从点B出发，以每秒4个单位长度的速度沿BC的方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于点D，作DE⊥AC于点E．F为射线CB上一点，使得∠CEF＝∠ABC．设点P运动的时间为x秒．
用含有x的代数式表示CE的长
求点F与点B重合时x的值
当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位)．求y与x之间的函数关系式