初中数学相似多边形的性质解答题

如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

（1）问题
如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．
求证：AD·BC=AP·BP．
（2）探究
如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
（3）应用
请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．

（1）问题情境：如图（1），已知，锐角∠AOB内有一定点P，过点P任意作一条直线MN，分别交射线OA、OB于点M、N．将直线MN绕着点P旋转，旋转过程中△MON的面积存在最小值．请问当直线MN在什么位置时，△MON的面积最小，并说明理由．

方法探究:小明与小亮二人一起研究，一会儿，小明说有办法了．小亮问：“怎么解决？”小明画出了图（2）的四边形，说：“四边形ABCD中，AD//BC，取DC边的中点E，连结AE并延长交BC的延长线于点F．显然有△ADE≌△FCE，则S_{四边形ABCD}=S_△ABF(S表示面积）．借助这图和图中的结论就可以解决了．”
请你照小明提供的方法完成“问题情境”这个问题．
（2）实际应用：如图（3），若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB 和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB = 70°，∠POB = 30°，OP= 4km，试求△MON 的面积．(结果精确到0.1km²)

（3）拓展延伸：如图（4），在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、（，）、（4，2），过点P的直线l与四边形OABC 一组对边相交，将四边形OABC分成两个四边形，则其中以点O为顶点的四边形的面积的最大值是               ．

（本题满分14分，第（1）小题满分4分，第（2）小题满分5分，第（3）小题满分5分）
已知：如图，是半圆的直径，弦，动点、分别在线段、上，且，的延长线与射线相交于点、与弦相交于点（点与点、不重合），，．设，的面积为．

（1）求证：；
（2）求关于的函数关系式，并写出它的定义域；
（3）当是直角三角形时，求线段的长．

如图，直线l经过点A（1，0），且与双曲线y＝（x＞0）交于点B（2，1），过点P（p，p－1）（p＞1）作x轴的平行线分别交曲线y＝（x＞0）和y＝－（x＜0）于M，N两点．

（1）求m的值及直线l的解析式；
（2）若点P在直线y＝2上，求证：△PMB∽△PNA；
（3）是否存在实数p，使得S_△AMN＝4S_△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．

（1）如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A（0，1），B（1，0）．在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=．

①求出E点的坐标（可用含m的代数式表示）；
②证明对于任意正数m，点E都在直线上；
（2）将（1）中的两个等腰直角三角形都改为有一个角为的直角三角形，如图22-2，A（0，），B（1，0）．Rt△ADE中， ∠ADE=，∠AED=．D（m，0）是x轴正半轴上任意一点，则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；
（3）将（2）中Rt△AOB保持不动，取点C（2， ），在x轴正半轴上取D（m，0）（m>2）， 然后在AD右上方作Rt△CDE， ∠CDE=，∠CED=．当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由．

我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．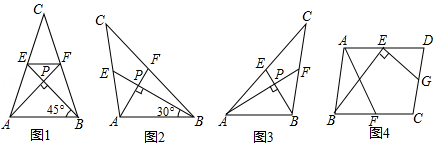

特例探索
（1）如图1，当∠ABE=45°，c=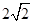时，a=      ，b=      ．
如图2，当∠ABE=30°，c=4时，a=      ，b=      ．
归纳证明
（2）请你观察（1）中的计算结果，猜想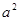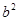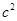，，三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．
拓展应用
（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=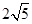，AB=3，求AF的长．

如图1，矩形ABCD的两条边在坐标轴上，点D与坐标原点O重合，且AD=8，AB=6．如图2，矩形ABCD沿OB方向以每秒1个单位长度的速度运动，同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动，当点P到达点C时，矩形ABCD和点P同时停止运动，设点P的运动时间为t秒．

（1）当t=5时，请直接写出点D、点P的坐标；
（2）当点P在线段AB或线段BC上运动时，求出△PBD的面积S关于t的函数关系式，并写出相应t的取值范围；
（3）点P在线段AB或线段BC上运动时，作PE⊥x轴，垂足为点E，当△PEO与△BCD相似时，求出相应的t值．

如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点
P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设点P的运动时间为x（秒）．

（1）用含有x的代数式表示CE的长；
（2）求点F与点B重合时x的值；
（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式；
（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．

如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B的坐标为（60，0），OA=AB，∠OAB=90°，OC=50．点P是线段OB上的一个动点（点P不与点O、B重合），过点P与y轴平行的直线l交边OA或边AB于点Q，交边OC或边BC于点R，设点P横坐标为t，线段QR的长度为m．已知t=40时，直线l恰好经过点C．

（1）求点A和点C的坐标；
（2）当0＜t＜30时，求m关于t的函数关系式；
（3）当m=35时，请直接写出t的值；
（4）直线l上有一点M，当∠PMB+∠POC=90°，且△PMB的周长为60时，请直接写出满足条件的点M的坐标．

在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN90°．
（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系．

如图，在▱ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将▱ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G．

（1）当点H与点C重合时．
①填空：点E到CD的距离是      ；
②求证：△BCE≌△GCF；
③求△CEF的面积；
（2）当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．

如图，在矩形ABCD中，AB=3，BC=4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P作PE∥DC，交AC于点E，动点P、Q的运动速度是每秒1个单位长度，运动时间为t秒，当点P运动到点A时，P、Q两点同时停止运动．

（1）用含有t的代数式表示PE=           ；
（2）探究：当t为何值时，四边形PQBE为梯形？
（3）是否存在这样的点P和点Q，使△PQE为等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．

（1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系： ．
（2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．
（3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．

如图，是坐标原点，矩形的顶点在轴的正半轴上，点在轴的正半轴上，点在边上，且点，．

（1）填空：的长为      ；
（2）若是的中点，将过点的直线绕旋转，分别与直线、相交于点、，与直线相交于点，连结．
①设点的纵坐标为．当∽时，求的值；
②试问：在旋转的过程中，线段与能否相等？若能，请求出的长；若不能，请说明理由．