初中数学相似多边形的性质解答题

我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均称为“中垂三角形”，设BC=a，AC=b，AB=c．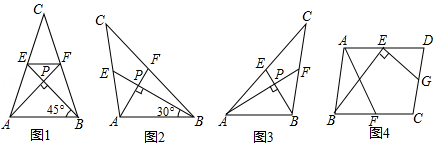

特例探索
（1）如图1，当∠ABE=45°，c=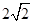时，a=      ，b=      ．
如图2，当∠ABE=30°，c=4时，a=      ，b=      ．
归纳证明
（2）请你观察（1）中的计算结果，猜想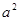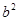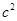，，三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．
拓展应用
（3）如图4，在▱ABCD中，点E、F、G分别是AD，BC，CD的中点，BE⊥EG，AD=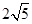，AB=3，求AF的长．

我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”．设BC＝a，AC＝b，AB＝c．
特例探索
（1）如图1，当∠ABE＝45°，c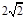＝时，a＝         ，b＝          ；
如图2，当∠ABE＝30°，c＝4时，a＝         ，b＝          ；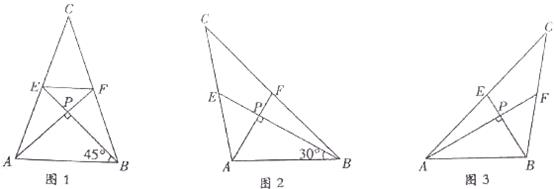

归纳证明
（2）请你观察（1）中的计算结果，猜想a²，b²，c²三者之间的关系，用等式表示出来，请利用图3证明你发现的关系式；
拓展应用
（3）如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD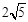＝，AB＝3．求AF的长．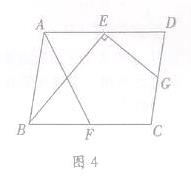

如图，在平面直角坐标系xOy中，将抛物线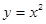的对称轴绕着点P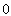（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.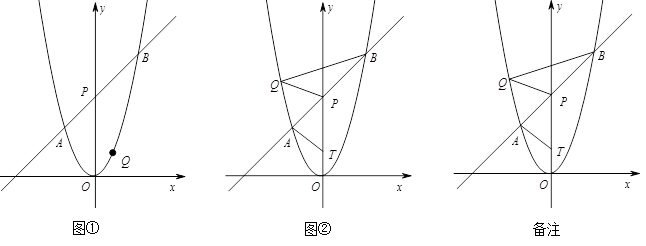

（1）求直线AB的函数表达式；
（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；
（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.

如图，在平面直角坐标系 $xOy$中，直线 $y=\frac{1}{2}x+2$与 $x$轴交于点 $A$，与 $y$轴交于点 $C$．抛物线 $y=a{x}^2+bx+c$的对称轴是 $x=-\frac{3}{2}$且经过 $A$、 $C$两点，与 $x$轴的另一交点为点 $B$．

（1）①直接写出点 $B$的坐标；②求抛物线解析式．
（2）若点 $P$为直线 $AC$上方的抛物线上的一点，连接 $PA,PC$．求 $△PAC$的面积的最大值，并求出此时点 $P$的坐标．
（3）抛物线上是否存在点 $M$，过点 $M$作 $MN$垂直 $x$轴于点 $N$，使得以点 $A$、 $M$、 $N$为顶点的三角形与 $△ABC$相似？若存在，求出点 $M$的坐标；若不存在，请说明理由．

（本小题满分13分）
（1）操作发现：如图①，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．直接写出线段AF与BD之间的数量关系．
（2）类比猜想：如图②，当△ABC为以BC为斜边的等腰直角三角形，D是△ABC边BA上一动点（点D 与点B不重合），连接DC，以DC为斜边在BC上方作等腰直角△FDC，连接AF．请直接写出它们的数量关系．
（3）深入探究：
Ⅰ．如图③，当△ABC为以BC为底边的等腰三角形，D是△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为底边在BC上方作等腰△FDC，∠BC A=∠DCF，且∠B A C =，连接AF．线段AF与BD之间的有什么数量关系？证明你发现的结论；
Ⅱ．如图④，当△ABC为任意三角形，D是△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作△FDC∽△ABC，且，连接AF．线段AF与BD之间的有什么数量关系？直接写出你发现的结论．

在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的反称点的定义如下：若在射线CP上存在一点P′，满足CP＋CP′＝2r.则称P′为点P关于⊙C的反称点，下图为点P及其关于⊙C的反称点P′的示意图.
特别地，当点P′与圆心C重合时，规定CP′＝0.

（1）当⊙O的半径为1时.
①分別判断点M（2，1），，关于⊙O的反称点是否存在？若存在，求其坐标；
②点P在直线y＝－x＋2上，若点P关于⊙O的反称点P′存在，且点P′不在x袖上，求点P的横坐标的取值范围；
（2）⊙C的圆心在x袖上，半径为1，直线与x轴、y轴分別交于点A，B.若线段AB存在点P，使得点P关于⊙C的反称点P′在⊙C的内部，求圆心C的横坐标的取值范围.

（本题8分）已知锐角△ABC中，边BC长为12，高AD长为8
（1）如图，矩形EFGH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K

①求的值
②设EH=x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值
（2）若ABAC，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，直接写出正方形PQMN的边长．

（1）如图1，等腰Rt△ABO放在平面直角坐标系中， 点A，B 的坐标分别是A（0，1），B（1，0）．在x轴正半轴上取D（m，0），在AD右上方作等腰Rt△ADE，∠ADE=．

①求出E点的坐标（可用含m的代数式表示）；
②证明对于任意正数m，点E都在直线上；
（2）将（1）中的两个等腰直角三角形都改为有一个角为的直角三角形，如图22-2，A（0，），B（1，0）．Rt△ADE中， ∠ADE=，∠AED=．D（m，0）是x轴正半轴上任意一点，则不论m取何正数，点E都在某一条直线上，请求出这条直线的函数关系式；
（3）将（2）中Rt△AOB保持不动，取点C（2， ），在x轴正半轴上取D（m，0）（m>2）， 然后在AD右上方作Rt△CDE， ∠CDE=，∠CED=．当m取不同值时，点E是否还是总在一条直线上? 若是，请求出直线对应的函数关系式，若不是，请说明理由．

如图1，在平面直角坐标系中，已知点A（－6，0），点B（0，8），点C在y轴上，将△OAB沿直线AC对折，使点O落在边AB上的点D处．

（1）求直线AB、AC的解析式．
（2）如图2，过B作BE⊥AC，垂足为E，若F为AB边上一动点，是否存在点F，使C为△EOF内心，若存在，请求出F点坐标，若不存在，请说明理由．

已知抛物线经过A（1，0）、B（3，0）、C（0，3）三个点，

（1）求抛物线的解析式；
（2）如图（1），作△OBC的外接圆⊙Oˊ，D为BC上方半圆上一点，当tan∠COD=时，求OD的长；
（3）如图（2）直线y=x-2与抛物线交于E、F两点，与y轴交于点G，作y轴的平行线，分别与线段EF、抛物线交于P、Q两点（点P与E、F不重合），点K为射线PE上一点，当△PQK与△BAC相似时，求△PQK的最大面积。

如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．
（2）如图③，在△ABC中，∠A＜∠B＜∠C．
①利用尺规作出△ABC的自相似点P（不写出作法，保留作图痕迹）；
②如果△ABC的内心P是该三角形的自相似点，请直接写出该三角形三个内角的度数．

如图，在同一平面上，两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4cm.

（1）填空：AD=  （cm），DC=  （cm）；
（2）点M，N分别从A点，C点同时以每秒1cm的速度等速出发，且分别在AD，CB上沿A→D，C→B的方向运动，当N点运动 到B点时，M，N两点同时停止运动，连结MN，求当M，N点运动了x秒时，点N到AD的距离（用含x的式子表示）；
（3）在（2）的条件下，取DC中点P，连结MP，NP，设△PMN的面积为y（cm²），在整个运动过程中，△PMN的面积y存在最大值，请求出这个最大值.
（参考数据：sin75°=，sin15°=）

在平面直角坐标系xoy中， 一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（－1，0）．

（1）请直接写出点B、C的坐标：B（  ，  ）、C（  ，  ）；并求经过A、B、C三点的抛物线解析式；
（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于第一象限的点M．
①设AE=x，当x为何值时，△OCE∽△OBC；
②在①被满足的情况下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．

如图①，△ABC与△DEF都是等腰直角三角形，∠ACB=∠EDF=90°，且点D在AB边上，AB、EF的中点均为O，连结BF、CD、CO，显然点C、F、O在同一条直线上，可以证明△BOF≌△COD，则BF=CD．
解决问题
（1）将图①中的Rt△DEF绕点O旋转得到图②，猜想此时线段BF与CD的数量关系，并证明你的结论；
（2）如图③，若△ABC与△DEF都是等边三角形，AB、EF的中点均为O，上述（1）中的结论仍然成立吗？如果成立，请说明理由；如不成立，请求出BF与CD之间的数量关系；
（3）如图④，若△ABC与△DEF都是等腰三角形，AB、EF的中点均为0，且顶角∠ACB=∠EDF=α，请直接写出的值（用含α的式子表示出来）

如图，矩形ABCD中，P是边AD上的一动点，连接BP、CP，过点B作射线交线段CP的延长线于点E，交AD边于点M，且使得∠ABE=∠CBP，如果AB=2，BC=5，AP=x，PM=y.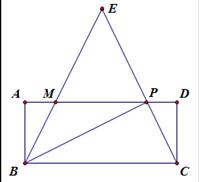

（1）说明△ABM∽△APB；并求出y关于x的函数关系式，写出自变量x的取值范围；
（2）当AP=4时，求sin∠EBP的值；
（3）如果△EBC是以∠EBC为底角的等腰三角形，求AP的长。