初中数学相似多边形的性质解答题

如图，直角三形纸片ABC中，∠ACB=90°，AC=6，BC=8．折叠该纸片使点B与点C重合，折痕与AB、BC的交点分别为D、E. 则sin∠DAE=    ．

如图，在⊙O的内接△ABC中，AD⊥BC于D，

（1）①若作直径AP，求证：AB·AC＝AD·AP；
②已知AB＋AC＝12，AD＝3，设⊙O的半径为y，AB的长为x．求y与x的函数关系式，及自变量x的取值范围；
（2）图2中，点E为⊙O上一点，且，求证：CE＋CD＝BD.

如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长交边AD于点F，交CD的延长线于点G．

（1）求证：△APB≌△APD；
（2）已知DF：FA=1：2，设线段DP的长为x，线段PF的长为y．
①求y与x的函数关系式；
②当x=6时，求线段FG的长．

如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．

（1）当t为何值时，∠AMN=∠ANM？
（2）当t为何值时，△AMN的面积最大？并求出这个最大值．

如图,已知在等腰△ABC中,∠A＝∠B＝30°.
(1)尺规作图：过点C作CD⊥AC交AB于点D；
过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；
(2)求证：.

如图，中，AB=AC=，，BD平分.

（1）图中有      个等腰三角形；
（2）求BC的长（用含的代数式表示）.

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点。

（1）求证：△ABE∽△ECM；
（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由；
（3）求当线段AM最短时的长度

在Rt△ABC中，∠C=90°，D为AB边上一点，点M、N分别在BC、AC边上，
且DM⊥DN，作MF⊥AB于点F，NE⊥AB于点E。
（1）特殊验证：如图1，若AC=BC，且D为AB中点，求证：DM=DN，AE=DF；
（2）拓展探究：若AC≠BC。
①如图2，若D为AB中点，（1）中的两个结论有一个仍成立，请指出并加以证明；
②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”，其它条件不变，请探究AE与DF的数量关系并加以证明。

如图在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC、直线和格点O.

（1）画出△ABC关于直线成轴对称的；
（2）画出将向上平移1个单位得到的；
（3）以格点O为位似中心，将作位似变换，将其放大到原来的两倍，得到.

如图，AB为⊙O的直径，弦CD与AB相交于E，DE=EC，过点B的切线与AD的延长线交于F，过E作EG⊥BC于G，延长GE交AD于H。
（1）求证：AH=HD；
（2）若，DF=9，求⊙O的半径。

）如图所示，在⊙O中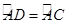，，弦AB与弦AC交于点A，弦CD与AB交于点F，连 接BC．
（1）求证：AC²=AB•AF；
（2）若⊙O的半径长为2cm，∠B=60°，求图中阴影部分面积．

如图，把一个矩形纸片ABCD沿AD和BC的中点连线EF对折，要使矩形AEFB与原矩形相似，且AB=6.

（1) 求AD的长。
（2）求矩形AEFB与原矩形ABCD的相似比。

如图，在□ABCD中，点E在BC边上，点F在DC的延长线上，且∠DAE=∠F．

（1）求证：△ABE∽△ECF；
（2）若AB=5，AD=8，BE=2，求FC的长．

如图1，ABCD中，AE⊥BC于E，AE=AD，EG⊥AB于G，延长GE、DC交于点F，连接AF．

（1）若BE=2EC，AB =，求AD的长；
（2）求证：EG=BG+FC；
（3）如图2，若AF=，EF=2，点是线段 AG上的一个动点，连接，将沿翻折得
，连接，试求当取得最小值时的长．