初中数学相似多边形的性质解答题

如图，中，AB=AC=，，BD平分.

（1）图中有      个等腰三角形；
（2）求BC的长（用含的代数式表示）.

（本题满分12分，每小题满分各6分）
已知：如图，平行四边形的对角线相交于点，点在边的延长线上，且，联结．

（1）求证：；
（2）如果，求证：．

在中，cm ，cm ，动点以1cm/s 的速度从点出发到点止，动点以2cm/s 的速度从点出发到点止，且两点同时运动，当以点、、为顶点的三角形与相似时，求运动的时间.

（本题7分）如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB中点，

（1）求证：AC²＝AB•AD；（2）求证：CE∥AD；（3）若AD＝4，AB＝6，求的值

）如图所示，在⊙O中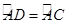，，弦AB与弦AC交于点A，弦CD与AB交于点F，连 接BC．
（1）求证：AC²=AB•AF；
（2）若⊙O的半径长为2cm，∠B=60°，求图中阴影部分面积．

如图△ABC中，AB=AC，∠A=120°

（1）用直尺和圆规作AB的垂直平分线，分别交BC，AB于点M，N（保留痕迹，不写作法）
（2）猜想CM与BM有何数量关系，并证明你的猜想。

如图1，ABCD中，AE⊥BC于E，AE=AD，EG⊥AB于G，延长GE、DC交于点F，连接AF．

（1）若BE=2EC，AB =，求AD的长；
（2）求证：EG=BG+FC；
（3）如图2，若AF=，EF=2，点是线段 AG上的一个动点，连接，将沿翻折得
，连接，试求当取得最小值时的长．

已知如图AD为△ABC上的高，E为AC上一点BE交AD于F且有BF=AC，FD=CD
求证：BE⊥AC

如图，两个同心圆的圆心为O，两圆的半径分别为5，3，其中A，B两点在大圆上，C，D在小圆上，且∠AOB=∠COD．
（1）求证：AC=BD；
（2）若∠AOB=120°，求线段AC，弧CD，线段BD，弧AB组成的封闭图形的面积；
（3）若AB与小圆相切，分别求AB，CD的长．

一条河的两岸有一段是平行的．在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆．在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽．

如图，在平行四边形ABCD中，E为BC边上的一点，连接AE、BD交于点F，AE＝AB.
（1）若∠AEB＝2∠ADB，求证：四边形ABCD是菱形.
（2）若AB＝10，BE＝2EC，求EF的长.

如图，在平行四边形ABCD中，的平分线分别与、交于点、．

（1）求证：；
（2）当时，求的值．

如图，已知矩形ABCD，AB=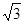，BC=3，在BC上取两点E，F（E在F左边），以时为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．

（1）求△PEF的边长；
（2）在不添加辅助线的情况下，当F与C不重合时，从图中找出一对相似三角形 （不含全等形），并证明；
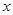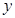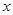（3）若△PEF的边EF在线段BC上以每秒1个单位的速度移动．设BE的长为，PH的长为，请你写出与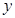的函数式，并指出函数自变量的取值范围．

如图，在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E．

（1）∠E=        度；
（2）写出图中现有的一对不全等的相似三角形，并说明理由；
（3）求弦DE的长．

如图1，在等腰直角△ABC中，∠BAC=90°，AB=AC=2，点E是BC边上一点，∠DEF=45°且角的两边分别与边AB，射线CA交于点P，Q.

（1）如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q.设BP为x，CQ为y，试求y与x的函数关系式，并写出自变量x的取值范围；
（2）如图3，点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．