如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F.求证:AO2=BO•OF.
如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(-3,0)、(-2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于 轴对称再向上平移1个单位后的图形△A1B1C1;
轴对称再向上平移1个单位后的图形△A1B1C1;
(3)在网格范围内,以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
如图,在平面直角坐标系中,点A(10,0),点C(0,6),,BC∥OA,OB=10,点E从点B出发,以每秒1个单位长度沿BC向点C运动,点F从点O出发,以每秒2个单位长度沿OB向点B运动,现点E、F同时出发,连接EF并延长交OA于点D,当F点到达B点时,E、F两点同时停止运动。设运动时间为t秒当四边形OCED是矩形时,求t的值;
当△BEF的面积最大时,求t的值;
当以BE为直径的圆经过点F时,求t的值;
当动点E、F会同时在某个反比例函数的图像上时,求t的值.(直接写出答案)

(本小题满分8分)如图,在一面与地面垂直的围墙的同一侧有一根高10米的旗杆AB和一个
高度未知的电线杆CD,它们都与地面垂直。为了测得电线杆的高度,一个小组的同学进行了如下测量:某
一时刻,在太阳光的照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10
米;而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米。依据这些数据,该
小组的同学计算出了电线杆的高度。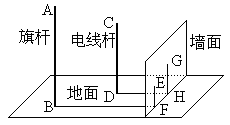
(1)该小组的同学在这里利用的是____________投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程。
阅读下面材料:小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.
(1)小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是 .
(2)参考小军思考问题的方法,解决问题:如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.
如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE.
(2)当E是AD的中点且BC=2CD时,求证:∠F=∠BCF.
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.
△ABC中,AB=AC.取BC边的中点D,作DE⊥AC于点E,取DE的中点F,连接BE,AF交于点H.
(1)如图1,如果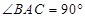 ,那么
,那么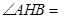 °,
°,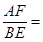 ;
;
(2)如图2,如果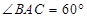 ,猜想
,猜想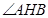 的度数和
的度数和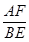 的值,并证明你的结论;
的值,并证明你的结论;
(3)如果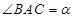 ,那么
,那么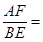 .(用含
.(用含 的表达式表示)
的表达式表示)
如图,四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO= ∠ACB;
∠ACB;
(2)若sin∠EAB= ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.
如图,△ABC中,BC >AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
试题篮
()