如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF="0°" 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF="30°" 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果 ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和 的值.
的值.
如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE ≌△OBG;
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;
(3)试求: 的值(结果保留根号).
的值(结果保留根号).
如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20㎝,求FC的长.
如图,梯形ABCD中DC∥AB,AB =2DC,对角线AC、BD相交予点O,BD =4。过AC的中点H作EF∥BD分别交AB、AD于点E、F,求EF的长
阅读下面材料:小军遇到这样一个问题:如图1,△ABC中,AB=6,AC=4,点D为BC的中点,求AD的取值范围.
(1)小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:AD的取值范围是 .
(2)参考小军思考问题的方法,解决问题:如图3,△ABC中,E为AB中点,P是CA延长线上一点,连接PE并延长交BC于点D.求证:PA•CD=PC•BD.
如图中小方格都是边长为1的正方形,△ABC和△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上。
(1)画出位似中心点O;
(2)△ABC与△A′B′C′的位似比为_______;
(3)以O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5。
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,且DG平分△ABC的周长,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△GBD ∽△GDF,求证:BG⊥CG.
△ABC中,AB=AC.取BC边的中点D,作DE⊥AC于点E,取DE的中点F,连接BE,AF交于点H.
(1)如图1,如果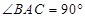 ,那么
,那么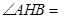 °,
°,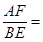 ;
;
(2)如图2,如果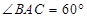 ,猜想
,猜想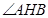 的度数和
的度数和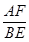 的值,并证明你的结论;
的值,并证明你的结论;
(3)如果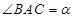 ,那么
,那么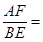 .(用含
.(用含 的表达式表示)
的表达式表示)
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO= ∠ACB;
∠ACB;
(2)若sin∠EAB= ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.
如图,△ABC中,BC >AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式.


如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3) .
.
(1)(3分)如图①,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.
求证:AB2=AD·AC;
(2)(4分)如图②,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC
于点F. ,求
,求 的值;
的值;
(3)(5分) 在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD
于点E,交直线AC于点F。若 ,请探究并直接写出
,请探究并直接写出 的所有可能的值(用含n的式子表
的所有可能的值(用含n的式子表
示),不必证明.
试题篮
()