初中数学相似多边形的性质解答题

如图，在Rt△ABC中，∠B=90°，AC=60，AB=30．D是AC上的动点，过D作DF⊥BC于F，过F作FE∥AC，交AB于E．设CD=x，DF=y．

（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△DEF是直角三角形时，求x的值．

如图，F在BD上，BC、AD相交于点E，且AB∥CD∥EF，

（1）图中有哪几对位似三角形，选其中一对加以证明；
（2）若AB＝2，CD＝3，求EF的长．

如图，已知在△ABC中，∠A = 90°，，经过这个三角形重心的直线DE // BC，分别交边AB、AC于点D和点E，P是线段DE上的一个动点，过点P分别作PM⊥BC，PF⊥AB，PG⊥AC，垂足分别为点M、F、G．设BM = x，四边形AFPG的面积为y．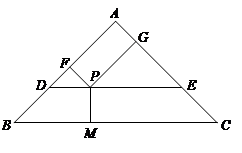

（1）求PM的长；
（2）求y关于x的函数解析式，并写出它的定义域；
（3）联结MF、MG，当△PMF与△PMG相似时，求BM的长．

如图和相交于点，，．

（1）如果的周长是9，求的周长；           
（2）连结，如果的面积是16，求的面积．

如图，在平行四边形ABCD中，点E在边BC上，联结AE并延长，交对角线BD于点F、DC的延长线于点G，如果．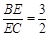

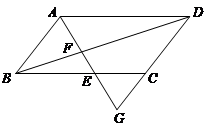
求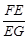的值．

如图△ABC中，DE∥BC，，M为BC上一点，AM交DE于N．

（1）若AE=4，求EC的长；
（2）若M为BC的中点，=36，求

如图，以△ABC的边AB为直径作⊙O，交BC于点D，且∠DAC=∠B．
（1）求证：AC是⊙O的切线；
（2）若点E是的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．

（本小题满分8分）（1）阅读理解
已知：如图1，△ABC中，AD是中线，点P在AD上，BP、CP的延长线分别交AC、AB于E、F．求证：EF∥BC．

证明：如图2，EF交AD于G,过P作MN∥BC分别交AB、AC于M、N，
在△ABD中，由PM∥BD，得到，同理，
因为BD=CD,所以PM=PN．
在△FBC中，由PM∥BC,所以同理，
，所以△EPF∽△CPB，所以∠FEP=∠PBC，所以EF∥BC．
（2）逆向思考
在△ABC中，D在BC上，点P在AD上，BP、CP的延长线分别交AC、AB于E、F，如果EF∥BC．那么D是BC中点．请你给出证明．
（3）知识应用
①如图3直线a、b、c、d、e、f、g、h是等距的一组平行线，AB在直线g上，请你用无刻度的直尺利用现有平行线作出线段AB的中点．并作简要的画图说明．
②如图4直线a、b、c、d、e、f、g、h是等距的一组平行线，点P不在这些直线上，点A在直线g上，点B在直线c上，请你用无刻度的直尺利用现有平行线作出过点P的直线PQ平行于AB．并作简要的画图说明．

已知：如图，在Rt△ABC中，∠A=90°，以AB为直径作⊙O，BC交⊙O于点D，E是边AC的中点，ED、AB的延长线相交于点F．
求证：（1）DE为⊙O的切线.
（2）AB•DF=AC•BF．

如图，在□ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

阅读下面的短文，并解答下列问题：
我们把相似形的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同．就把它们叫做相似体．
如图，甲、乙是两个不同的正方体，正方体都是相似体，它们的一切对应线段之比都等于相似比：a：b，设S_甲：S_乙分别表示这两个正方体的表面积，则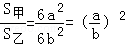，又设V_甲、V_乙分别表示这两个正方体的体积，则．
（1）下列几何体中，一定属于相似体的是　_________　

A．两个球体；

B．两个圆锥体；

C．两个圆柱体；

D．两个长方体．

（2）请归纳出相似体的3条主要性质：
①相似体的一切对应线段（或弧）长的比等于　_________　；
②相似体表面积的比等于　_________　；
③相似体体积的比等于　_________　．

如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．

（1）求证：KE=GE；
（2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；
（3）在（2）的条件下，若sinE=，AK=，求FG的长．

如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点．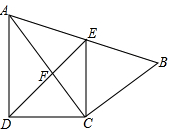

（1）求证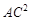：=AB·AD；
（2）若AD=4，AB=6，求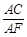的值．

如图1，在△ABC中，∠ACB=90°，经过点B的直线l（l不与直线AB重合）与直线BC的夹角的大小等于∠ABC，分别过点C、A作直线l的垂线，垂足分别为点D、E

（1）写出线段AE、CD之间的数量关系，并加以证明；
（2）当△ABC的位置旋转到图2或图3时，设直线CE、AB交于点F，且，CD=4，请你在图2和图3中任选一种情况，求此时BD的长．

在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE=∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．
（1）当点P与点C重合时（如图1）．求证：△BOG≌△POE；
（2）结合图2，通过观察、测量、猜想：=______，并证明你的猜想；
（3）把正方形ABCD改为菱形，其他条件不变（如图3），若AC=8，BD=6，直接写出的值．