初中数学相似多边形的性质解答题

如图，已知：矩形ABCD，以对角线AC的中点O为圆心，OA的长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为点K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．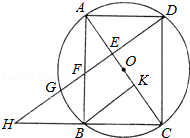

（1）求证：AE=CK；
（2）若F是EG的中点，且DE=6，求⊙O的半径．

如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D，交BC于点E．

（1）求证：BD=ID；
（2）求证：ID²=DE•DA．

如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

（1）求证：∠B=∠D；
（2）若AB=4，BC﹣AC=2，求CE的长．

如图，在Rt△ACB中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动，它们的速度都是1米/秒，问：几秒后△PCQ的面积为Rt△ACB面积的一半？

如图，在直角坐标系中，△ABO三个顶点及点P的坐标分别是O（0，0），A（4，2），B（2，4），P（4，4），以点P为位似中心，画△DEF与△ABO位似，且相似比为1：2，请在网格中画出符合条件的△DEF．

如图，△ABC中，AB=AC，BE⊥AC于E，D是BC中点，连接AD与BE交于点F，求证：△AFE∽△BCE．

已知线段AB，只用圆规找AB的中点P．

作法：
（1）以A为圆心，AB长为半径作圆；
（2）以B为圆心，AB长为半径在圆上连续截取，记截点为B₁，B₂，B₃，B₄，B₅；
（3）以B₃为圆心，BB₃长为半径画弧；以B为圆心，AB长为半径画弧，与前弧交于点C；
（4）以C为圆心，CB长为半径画弧交线段AB于点P．
结论：点P就是所求作的线段AB的中点．
（1）配合图形，理解作法，根据作图过程给予证明：点P是线段AB的中点．
（2）已知⊙O，请只用圆规把圆周四等分．（保留作图痕迹，不要求写作法）

如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作⊙O的切线交边BC于N．

（1）图中是否存在与△ODM相似的三角形，若存在，请找出并给予证明；
（2）设DM=x，OA=R，求R关于x的函数关系式；
（3）在动点O逐渐向点D运动（OA逐渐增大）的过程中，△CMN的周长如何变化？说明理由．

如图，△ABC中，AB=8厘米，AC=16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以A、P、Q为顶点的三角形与△ABC相似时，运动时间是多少？

已知：如图①，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：

（1）当t为何值时，PQ∥BC；
（2）设△AQP的面积为y（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

（1）如图①，在Rt△ABC中，∠ABC=90°，BD⊥AC于点D．求证：AB²=AD•AC；
（2）如图②，在Rt△ABC中，∠ABC=90°，点D为BC边上的点，BE⊥AD于点E，延长BE交AC于点F．=1，求的值；
（3）在Rt△ABC中，∠ABC=90°，点D为直线BC上的动点（点D不与B、C重合），直线BE⊥AD于点E，交直线AC于点F．若=n，请探究并直接写出的所有可能的值（用含n的式子表示），不必证明．

如图，在⊙O中，弦AB与弦CD相交于点G，OA⊥CD于点E，过点B的直线与CD的延长线交于点F，AC∥BF．

（1）若∠FGB=∠FBG，求证：BF是⊙O的切线；
（2）若tan∠F=，CD=a，请用a表示⊙O的半径；
（3）求证：GF²-GB²=DF•GF．

在△ABC中，点D在直线AB上，在直线BC上取一点E，连接AE，DE，使得 AE=DE，DE交AC于点G，过点D作DF∥AC，交直线BC于点F，∠EAC=∠DEF．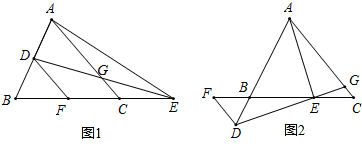

（1）当点E在BC的延长线上，D为AB的中点时，如图1所示．
①求证：∠EGC=∠AEC；
②若DF=3，求BE的长度；
（2）当点E在BC上，点D在AB的延长线上时，如图2所示，若CE=10，5EG=2DE，求AG的长度．

问题引入：如图，在△ABC中，D是BC上一点，AE=AD，求：
尝试探究：过点A作BC的垂线，垂足为F，过点E作BC的垂线，垂足为G，如图所示，有，，．
类比延伸：若E为AD上的任一点，如图所示，试猜S_{四边形ABEC}与S_△ABC的比是图中哪条线段的比，并加以证明．
拓展应用：如图，E为△ABC内一点，射线AE于BC于点D，射线BE交AC于点F，射线CE交AB于点G，求的值．

将边长为8cm的正方形纸片ABCD沿EG折叠（折痕EG分别与AB、DC交于点E、G），使点B落在AD边上的点 F处，FN与DC交于点M，连接BF与EG交于点P．

（1）当点F与AD的中点重合时（如图1）：
①△AEF的边AE=         cm，EF=          cm，线段EG与BF的大小关系是EG           BF；（填“＞”、“=”或“＜”）
②求△FDM的周长．
（2）当点F在AD边上除点A、D外的任意位置时（如图2）：
③试问第（1）题中线段EG与BF的大小关系是否发生变化？请证明你的结论；
④当点F在何位置时，四边形AEGD的面积S最大？最大值是多少？