如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D.若CD=CF,则 .
. 
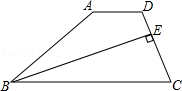
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是 .
如图9是置于水平地面上的一个球形储油罐,小敏想测量它的半径.在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(即AB=10米);同一时刻,他又测得竖直立在地面上长为1米的竹竿的影子长为2米,则球的半径是_ 米.
(11·天水)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做
了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜
子放在离树(AB)8.7m的点E处,然后观测考沿着直线BE后退到点D,这时恰好在镜子里
看到树梢顶点A,再用皮尺量得DE=2.7m,观测者目高CD=1.6m,则树高AB约是_
▲ .(精确到0.1m)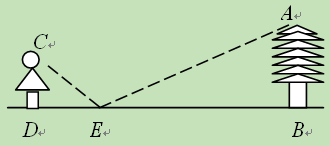
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥A B,EF∥AC,
B,EF∥AC,
得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边
形E1D1FF1,它的面积记作S2.照此规律作下去,则S2011= .
如图所示,在梯形ABCD中,AD∥BC,CE是∠BCD的平分线,且CE⊥AB,E为垂足,BE=2AE,若四边形AECD的面积为1,则梯形ABCD的面积为( )
在比例尺1∶10 000 000的地图上,量得甲、乙两个城市之间的距离是8 cm,那么甲、乙两个城市之间的实际距离应为 km。
、若四边形ABCD与四边形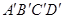 的相似比为3∶2,那么四边形
的相似比为3∶2,那么四边形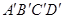 与四边形ABCD的相似比为 。
与四边形ABCD的相似比为 。
、已知两个相似园形的相似比是3∶4,其中一个园形的半径长为4 cm,那么另一个园形的半径长为 。
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC= CE,F、G分别是BC、CE的中点,FM∥AC,GE∥DC、设图中三个平行四边形的面积依次是
CE,F、G分别是BC、CE的中点,FM∥AC,GE∥DC、设图中三个平行四边形的面积依次是 、
、 、
、 ,若
,若 ,则
,则 = .
= .
、如图,四边形ABCD和四边形A1B1C1D1相似,已知∠A=120°,∠B=85°
∠C1=75°,AB=10,A1B1=16,CD=18,则∠D1= ,C1D1= ,它们的相似比为 。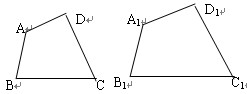
如图,在正六边形ABCDEF与正六边形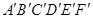 中
中
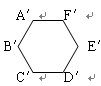
∵正六边形的每个内角都等于120°
∴∠A=∠A′, , ,
, , ;
又∵AB=BC=CD=DE=EF=FA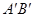 = ;
= ;
∴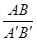 = '
= '
∴正六边形ABCDEF∽正六边形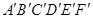
试题篮
()