初中数学相似多边形的性质试题

如图，点为轴正半轴上一点，两点关于轴对称，过点任作直线交抛物线于，两点

（1）求证：∠=∠；
（2）若点的坐标为（0，1），且∠=60º，试求所有满足条件的直线的函数解析式.

如图，在Rt△ABC中，斜边AB的长为35，正方形CDEF内接于△ABC，且其边长为12，则△ABC的周长为        .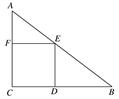

如图所示 ，在等边中，D、E分别是AB、AC上的点，，如图（1），然后将绕A点顺时针旋转，使B、A、E三点在同一直线上，得到图（2），M、N分别是BD、CE的中点，连接AM、AN、MN得到图（3），请解答下列问题：
（1）在图（2）中，线段BD与线段CE的大小关系是                         ；
（2）在图（3）中，与是相似三角形吗？请证明你的结论。

如图，在4×4的方格纸中，和的顶点都在格点上。
（1）填空：            度；            ；

（2）判断与是否相似，请证明你的结论。

如图，在中，若，，，求BC的长.

如图，在方格纸上，与是关于点O为位似中心的位似图形，他们的顶点都在格点上．

（1）画出位似中心O；
（2）求出与的位似比；
（3）以O点为位似中心，再画一个使它与的位似比等于3

若∽，，，则的度数为              ．

已知两点，，且，则点的C坐标为

A．

B．

C．

D．

下列两个图形一定相似的是

A．任意两个等腰梯形

B．任意两个菱形

C．任意两个正方形

D．任意两个矩形

在一张复印机复印出来的纸上，一个多边形图案的一条边由原来的1cm变成2cm，那么这次复印出来的多边形图案面积是原来的

A．1倍

B．2倍

C．3倍

D．4倍

在平面直角坐标系xOy中,反比例函数的图象与抛物线 
交于点A(3, n).
（1）求n的值及抛物线的解析式；
（2） 过点A作直线BC，交x轴于点B，交反比例函数（）的图象于点C，且AC=2AB，求B、C两点的坐标；                              
（3）在（2）的条件下，若点P是抛物线对称轴上的一点，且点P到x轴和直线BC的距离相等，求点P的坐标.

（本小题满分4分）
如图，已知每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形. 图中的△ABC是一个格点三角形.

（1）请你在第一象限内画出格点△AB₁C₁， 使得△AB₁C₁∽△ABC，且△AB₁C₁与△ABC的相似比为3：1；
（2）写出B₁、C₁两点的坐标.

(本小题满分5分)
已知：如图，在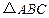中，D是AC上一点，联结BD，且∠ABD =∠ACB.

（1）求证：△ABD∽△ACB；
（2）若AD=5，AB= 7，求AC的长.

如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，求CF的长 .

如图，⊙O是△ABC的外接圆，BC是⊙O的直径，

O

D是劣弧中点，BD交AC于点E.

                          
⑴求证：AD²=DE·DB
⑵若BC=13，CD=5，求DE的长